考研数学三（常微分方程与差分方程）模拟试卷40

考研数学三（常微分方程与差分方程）模拟试卷40

选择题

1.方程y”＝－1／3x²的通解是________.(B)

A. lnC₁x／3＋C₂

B. lnC₁x／3＋C₂x

C. 2x＋lnC₁x^1／3＋C₂

D. lnC₁x／3＋2xC₂

解析：直按把A、B、C、D四个选项代入原方程知A、B、C均为方程的解，但仅B中含两个独立的任意常数，而A、C中实际上仅含一个任意常数，故应选B.

2.若连续函数f(x)满足关系式f(x)＝∫₀^2xf(t／2)dt＋ln2，则f(x)＝________．(B)

A. e^xln2

B. e^2xln2

C. e^x＋ln2

D. e^2x＋ln2

解析：所给关系式网边对x求导得f’(x)＝2f(x)，从而f(x)＝Ce^2x，又在x＝0处原关系式给出f(0)＝ln2，代入上述表达式得C＝ln2.因此f(x)＝e^2xln2.

当然，逐一验证也可得到B为正确选项.

故应选B.

3.已知函数y＝y(x)在任意点x处的增量y＝y△x／(1＋x²)＋α，且当△x→0时，α是△x的高阶无穷小，y(0)＝π，则y(1)＝________.(D)

A. 2π

B. π

C. e^π／4

D. πe^π／4

解析：由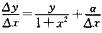

填空题

4.已知曲线y＝f(x)过点(0，－1／2)，且其上任一点(x，y)处的切线斜率为xln(1＋x²)，则f(x)＝________．

(1＋x²)[ln(1＋x²)－1]／2＋C

解析：由y’＝xln(1＋x²)得

dy＝xln(1＋x²)dx.

等式两端积分得

y＝∫xln(1＋x²)dx＝(1＋x²)[ln(1＋x²)－1]／2＋C.

把(0，－1／2)代入上式，得C＝0.

故应填(1＋x²)[ln(1＋x²)－1]／2＋C.

5.微分方程y’＝[y(1－x)]／x的通解是________．

Cx．e^－x

解析：原方程化为dy／y＝(1／x－1)dx，即

lny＝lnx－x＋lnC＝ln(Cx)－x，整理得y＝Cx.e^－x.

故应填y＝Cx．e^－x.

6.微分方程ydx＋(x²－4x)dy＝0的通解为________．

(x－4)y⁴＝Cx

解析：分离变量得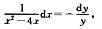

等式两端积分得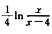

解答题

求关于给定的原始式所满足的微分方程:

7.y＝Ax²＋Bx＋C.其中A、B、C为任意常数.

由于原始式有三个独立的任意常数，考虑如下四个方程:

y＝Ax²＋Bx＋C，

dy／dx＝2Ax＋B，

d²y／dx²＝2A.

d³y／dx³＝0，，

最后一个方程d³y／dx³＝0没有任意常数，且恰为三阶微分方程，即为所求.

解析：

8.y＝Acosax＋Bsinax，A、B为任意常数，a为一周定常数.

由于y＝Acosax＋Bsinax，则dy／dx＝－Aasinax＋Bacosax.

d²y／dx²＝－Aa²cosax－Ba²sinax＝－a²(Acosax＋Bsinax)＝－a²y.

故所求微分方程为

d²y／dx²＋a²y＝0.

解析：

9.求以y＝C₁e^x＋C₂e^－x－x为通解的微分方程(C₁、C₂为任意常数).

由y＝C₁e^x＋C₂e^－x－x，对x求导得

y’＝C₁e^x－Ce^－x－1，①

上式再对x求导得

y”＝C₁e^x＋C₂e^－x，②

由①式与②式得y＝y”－x即所求微分方程为y”－y－x＝0.

解析：

写出由下列条件确定的曲线所满足的微分方程:

10.曲线在点(x，y)处的切线的斜率等于该点横坐标的平方；<

本文档预览：3000字符，共8423字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载