
考研数学一(高等数学)模拟试卷431
选择题
1.设f(x)=∫0sin xsin t2dt,g(x)=x3+x4,当x→0时,f(x)是g(x)的( ).(B)
A. 等价无穷小
B. 同阶但非等价的无穷小
C. 高阶无穷小
D. 低阶无穷小
解析:因为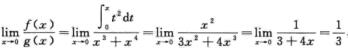
2.函数f(x)在x=1处可导的充分必要条件是( ).(D)
A. 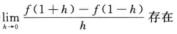 B.
B. 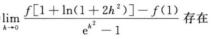 C.
C. 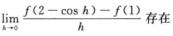 D.
D. 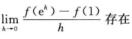 解析:A不正确,例如:
解析:A不正确,例如: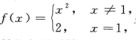 显然
显然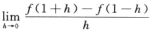 存在,但f(x)在x=1处不连续,所以也不可导;B不正确,因为
存在,但f(x)在x=1处不连续,所以也不可导;B不正确,因为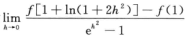 存在只能保证f(x)在x=1处右导数存在;C不正确,因为
存在只能保证f(x)在x=1处右导数存在;C不正确,因为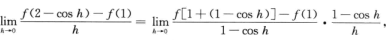
而 ,所以
,所以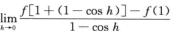 不一定存在,于是f(x)在x=1处不一定右可导,也不一定可导;
不一定存在,于是f(x)在x=1处不一定右可导,也不一定可导;
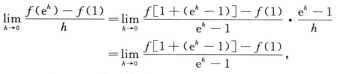
上式极限存在
3.设f(x)在[a,+∞)上二阶可导,f(a)<0,f’(a)=0,且f’’(x)≥k(k>0),则f(x)在(a,+∞)内的零点个数为( ).(B)
A. 0个
B. 1个
C. 2个
D. 3个
解析:因为f’(a)=0,且f’’(x)≥k(k>0),所以f(x)=f(a)+f’(a)(x-a)+f’(ξ)/2!(x-a)2≥f(a)+k/2(x-a)2,其中拿介于a与x之间.而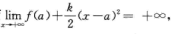
故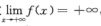
4.设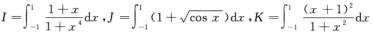 (D)
(D)
A. J<I<K
B. I<J<K
C. K<I<J
D. I<K<J
解析: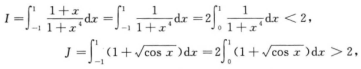
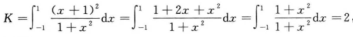
5.设z=f(x,y)为连续函数,且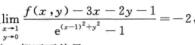 (D)
(D)
A. f(x,y)在(1,0)处对x对y都不可偏导
B. f(x,y)在(1,0)处对x可偏导,对y不可偏导
C. f(x,y)在(1,0)处对y可偏导,对x不可偏导
D. f(x,y)在(1,0)处可微,且dz|(1,0)=3dx+2dy
解析:令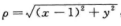 ,由
,由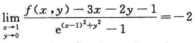 得f(1,0)=4.
得f(1,0)=4.
再由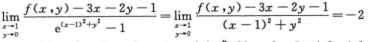
6.设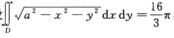 (B)
(B)
A. 1
B. 2
C
本文档预览:3000字符,共15184字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载
