考研数学一（高等数学）模拟试卷433

考研数学一（高等数学）模拟试卷433

选择题

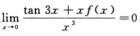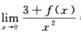1.设f(x)连续，且，则(C)

A. -27

B. 27

C. -9

D. 9

解析：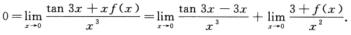

由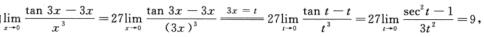

得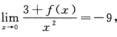

2.设f(x)在x=a处二阶可导，则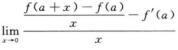(D)

A. -f’’(a)

B. f’’(a)

C. 2f’’(a)

D. 1／2f’’(a)

解析：由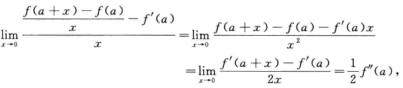

3.曲线(D)

A. 0条

B. 1条

C. 2条

D. 3条

解析：因为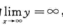，所以曲线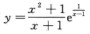无水平渐近线；

由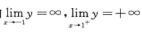，得曲线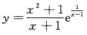有两条铅直渐近线；

由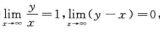，得曲线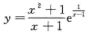

4.反常积分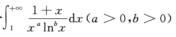(D)

A. a＞1，b＞1

B. a＞1，b＜1

C. a＞2，b＞1

D. a＞2，b＜1

解析：由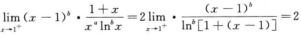得0＜b＜1；

由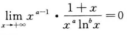

5.微分方程y’’+y’-2y=x²+1+xe^x的特解形式为( )．(D)

A. y₀=ax²+bx+c+(Ax+B)e^x

B. y₀=x(ax²+bx+C)+(Ax+B)e^x

C. y₀=x(ax²+bx+C)+x(Ax+B)e^x

D. y₀=ax²+bx+C+z(Ax+B)e^x

解析：y’’+y’-2y=0的特征方程为λ²+λ-2=0，即特征值为λ₁=1，λ₂=-2，令

y’’+y’-2y=x²+1， (1)

y’’+y’-2y=xe^x， (2)

(1)的特解形式为y₁=ax²+bx+c；(2)的特解形式为y₂=x(Ax+B)e^x，原方程的特解形式为y₀=ax²+bx+c+x(Ax+B)e^x，选D．

6.设幂级数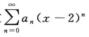在x=6处条件收敛，则幂级数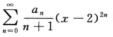(A)

A. 2

B. 4

C. 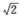D. 无法确定

解析：因为本文档预览：3000字符，共13384字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载