考研数学一（高等数学）模拟试卷393

考研数学一（高等数学）模拟试卷393

选择题

1.若方程x—e1nx—k=0在(0，1]上有解，则k的最小值为( )．(C)

A. —1

B. 1/e

C. 1

D. e

解析：记f(x)=x—eln x—k，则 f’(x)=1—e/x＜0，x∈(0，1]，这表明f(x)在(0，1]上单调递减，因而它在(0，1]上最多只有—个零点．

又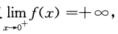由极限的保号性，存在r，0＜r＜1，使得f(r)＞0．f(x)在[r，1]上连续，f(r)＞0，f(1)=1—k．

当f(1)=1—k=0，即k=1时，x=1是f(x)的—个零点，即x=1是方程z—e1n x—k=0的—个解．

当f(1)=1—k＜0，即k＞1时，由在闭区间上连续函数的零点定理，知函数f(x)在(r，1)

2.若反常积分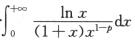(C)

A. p＜1

B. p＞1

C. 0＜P＜1

D. 0≤P＜1

解析：此积分为有—个瑕点x=0的无穷区间上的反常积分，可写为

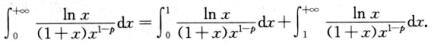
对任意ε＞0，有

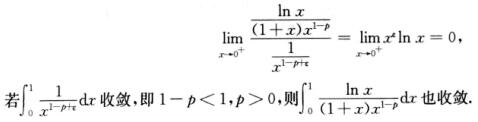
对任意ε＞0，有

3.曲线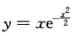(C)

A. 1

B. 2

C. 3

D. 4

解析：曲线方程的—阶导和二阶导分别为

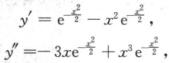
令y’’=0，得x=0，x=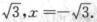列表如下．

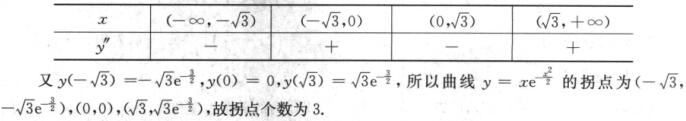
4.若可导函数f(x)满足f’(x)＜2f(x)，则当b＞α＞0时，有( )．(B)

A. b²f(α)＞α²f(b)

B. b²f(1n α)＞α²f(1n b)

C. b²f(α)＜α²f(b)

D. b²f(1n α)＜α²f(1n b)

解析：令φ(x)=e^—2xf(x)，则由题设知，φ’(x)=e^—2x[f’(x)—2f(x)]＜0，故φ(x)单调减少．于是，当b＞α＞0时，φ(1n b)＜φ(1n α)，即e^—21nbf(1n b)＜e^{—21n α}f(1nα)，也即b^—2f(1n b)＜α^—2f(1n α)，由此即得b²f(1n α)＞α²f(1n b)．

由题干条件无法确定b²f(α)与α²f(b)的大小关系，如f(x)=e^x，则f’(x)=e^x＜2e^x=2f(x)．

令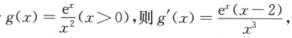

5.设Ⅰ₁=∫₀¹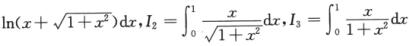(C)

A. Ⅰ₁＜Ⅰ₂＜Ⅰ₃

B. Ⅰ₁＜Ⅰ₃＜Ⅰ₂

C. Ⅰ₃＜Ⅰ₂＜Ⅰ₁

D. Ⅰ₃＜Ⅰ₁＜Ⅰ₂

解析：利用定积分的性质：若f(x)，g(x)在[α，b]上连续，且f(x)≤g(x)，则∫_α^bf(x)dx≤∫_α^bg(x)dx；若还存在点x₀∈[α，b]，使得f(x₀)＜g(x₀)，则∫_α^bf(x)dx＜∫_α^bg(x)dx．

记F(x)=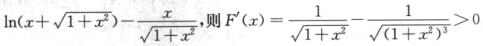，所以F(x)在[0，+∞)上严格单调递增，故当x＞0时，F(x)＞F(0)=0，即．

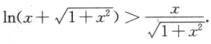另外，显然有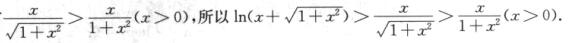

6.设f(x)在x=0处二阶可导，f(0)=0且本文档预览：3000字符，共10013字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载