考研数学一（高等数学）模拟试卷392

考研数学一（高等数学）模拟试卷392

选择题

1.设函数f(x)=x(2x—3)(4x—5)，则方程f’(x)=0的实根个数为( )．(C)

A. 0

B. 1

C. 2

D. 3

解析：

2.下列反常积分中，发散的是( )．

(D)

A.

B.

C.

D.

解析：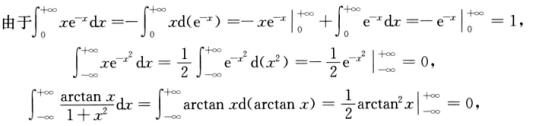

所以选项A，B，C中的积分都是收敛的，而

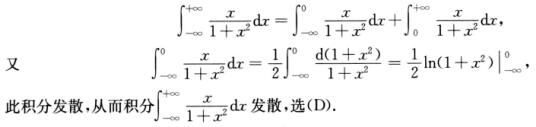
3.设某人在x=0时，从静止开始运动，其速度曲线为f₁(x)，加速度曲线为f₂(x)，且速度函数在[x，x+1]上的平均值函数曲线为f₃(x)，x表示时间，则以下3条曲线

(B)

A. f₁(x)=y₂(x)，f₂(x)=y₁(x)，f₃(x)=y₃(x)

B. f₁(x)y₂(x)，f₂(x)=y₃(x)，f₂(x)=y₁(x)

C. f₁(x)=y₃(x)，f₂(x)=y₂(x)，f₃(x)=y₁(x)

D. f₁(x)=y₃(x)=f₂(x)=y₁(x)，f₃(x)=y₂(x)

解析：由题意知，f₂(x)=f’₁(x)，f₃(x)=∫_x^x+1f₁(t)dt．

方法— 当x=0时，速度函数f₁(0)=0，故f₁(x)=y₂(x)，排除选项C，D．由于f₃(x)=

∫_x^x+1f₁(t)dt=∫_x^x+1y₂(t)dt=y₂(ξ)＞0(ξ介于x，x+1之间)，而y₃(x)中有小于0的部分，故排除A．

4.设x≥0，y≥0，曲线ι₁：x²+y²—xy=1，ι₂：x²+y₂—xy=2，直线ι₃：y=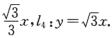．区域D₁由ι₁，ι₂，x=0，y=0围成，D2由ι₁，ι₂，ι₃，y=0围成，D₃由ι₁，ι₂，ι₄，x=0围成，则对于I_i=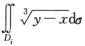(D)

A. Ⅰ₁＜Ⅰ₂＜Ⅰ₃

B. Ⅰ₃＜Ⅰ₁＜Ⅰ₂

C. Ⅰ₂＜Ⅰ₃＜Ⅰ₁

D. Ⅰ₂＜Ⅰ₁＜Ⅰ₃

解析：ι₁，ι₂，ι₃，ι₄的图形如图所示．

由于区域D₁关于y=x对称，由轮换对称性得

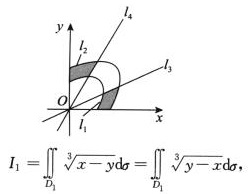
故Ⅰ₁=0．

由于D₂在y=x的下侧，故y＜x，则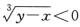；由于D₃在y=x的上侧，故y＞x，则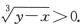

5.设连续型随机变量X的分布函数为F(x)=0．4φ(2x-1)+0．6φ(x／2-1)，则E(X²)=( )．(D)

A. 2

B. 3

C. 4

D. 5

解析：X的密度函数为f(x)=0．8φ(2x-1)+0．3φ(x／2-1)，则

E(X²)=0．8∫_-∞^+∞x²φ(2x-1)dx+0．3∫_-∞^+∞x²φ(x／2-1)dx

=

本文档预览：3000字符，共10928字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载