考研数学三（常微分方程与差分方程）模拟试卷45

考研数学三（常微分方程与差分方程）模拟试卷45

选择题

1.已知y＝x／lnx是微分方程y’＝y／x＋φ(x／y)的解，则φ(x／y)的表达式为________．(A)

A. －y²／x²

B. y²／x²

C. －x²／y²

D. x²／y²

解析：将y＝x／lnx代入微分方程y’＝y／x＋φ(x／y)，得

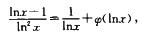
填空题

2.欧拉方程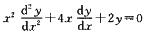

y＝C₁／x＋C₂／x²

解析：令x＝e^t，则

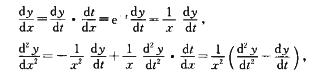
代入原方程，整理得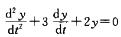

3.微分方程xy’＋y＝0满足初始条件y(1)＝2的特解为________．

xy＝2

解析：原方程可化为(xy)’＝0，积分得xy＝C，代入初始条件得C＝2，从而所求特解为xy＝2.

故应填xy＝2.

4.已知f²(x)＝∫₀^x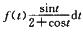

f(x)＝－ln|2＋cosx|／2＋ln3／2＋1

解析：对已知等式两端关于x求导，得

2f(x)f’(x)＝f(x)sinx／(2＋cosx).

整理得f’(x)＝sinx／2(2＋cosx)，则

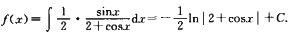
解答题

5.长为6米的链条自桌上无摩攮地向下滑动，假设运动开始时，链条自桌上垂下部分已有1米长，试问，需要多长时间，链条才全部滑离桌面?

取桌面为x轴的原点，x轴的方向垂直向下，设在时刻t时销条在桌面下端的长度为x，则x＝x(t)，再设链条的线密度为ρ(ρ为常数)，于是在时刻t，作用在链条上的力是重力ρxg(g为重力加速度)，因此有

[*]

且满足x(0)＝1，x’(0)＝0.

由特征方程r²－g／6＝0，得特征根r＝[*]，于是方程的通解是

[*]

再由x(0)＝1，x’(0)＝0，可得C₁＝C₂＝1／2，所以

[*]

当x＝6时，可得[*]所以，链条全部滑离桌面所需的时间为

[*]

解析：

6.求方程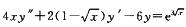

令[*]＝u，则

[*]

代入原方程可得[*]，其通解为:

y＝C₁e^3u＋C₂e^－2u＋ue^3u／5.

[*]

解析：

7.设函数y＝y(x)由方程(1＋x)y＝∫₀^x[2y＋(1＋t)²y”(t)]dt－ln(1＋x)

所确定，其中x≥0，且y’|_x＝0＝0，试求y(x).

将方程两边求导，得

y＋(1＋x)y’＝2y＋(1＋x)²y”－1／(1＋x).

有初值问题

[*]

令1＋x＝e^t，记D＝d／dt，有D(D－1)y－Dy＋y＝e^－t，即为y”_t－2y’_t＋y＝e^－t，特征方程为.

λ²－2λ＋1＝0得λ_1，2＝1，

齐次方程通解为

y＝(C₁＋C₂t)e^t.

由f(t)＝e^－t，λ＝－1不是特征根，故可设一特解y^*＝Ae^－t，代入得A＝1／4.故通解为

[*]

把y|_x＝0＝0，y’|_x＝0＝0代入得

C₁＝－1／4，C₂＝1／2．

故原方程的解为

[*]

解析：

8.用幂级数求微分方程(1－x)y’＝x²－y的解.

设方程解为[*]代入原方程得

[*]

比较两端系数，求出原方程通解为

[*]

解析：

9.用幂级数求微分方程(x＋1)y’＝x²－2x＋y的解.

设方程解为[*]代入原方程得

[*]

比较两端系数，求出原方程通解为

[*]

解析：

10.用幂级数求y’＝y²＋x

本文档预览：3000字符，共10232字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载