考研数学一（线性代数）模拟试卷169

考研数学一（线性代数）模拟试卷169

选择题

1.多项式f(x)=(C)

A. 2

B. 4

C. 6

D. 8

解析：要求多项式的常数项，只需令x=0求行列式的值即可，故

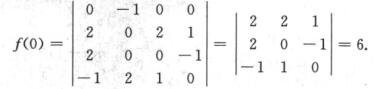
2.已知矩阵方程A=BC，其中A=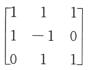，则B，C可以是( )．

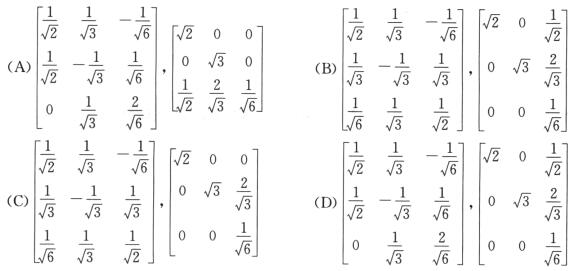(D)

A.

B.

C.

D.

解析：在考研范围内，可认为本题考查矩阵相乘的运算规则。

D选项符合题意．

事实上，A选项中左边矩阵第1行乘右边矩阵第1列得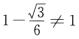，不符合题意，排除；

B，C选项中左边矩阵第3行乘右边矩阵第1列得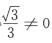

3.设A为2阶方阵，B为3阶方阵，|A|=2，|B|=3，C=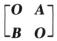，则C^*=( )．

(D)

A.

B.

C.

D.

解析：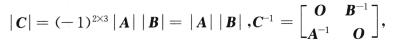

故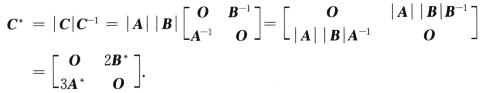

4.设A，B是3阶矩阵，A是非零矩阵，且满足AB=0,B=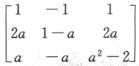(D)

A. α=—1，必有r(A)=1

B. α=2，必有r(A)=2

C. α=—1，必有r(A)=2

D. α=2，必有r(A)=1

解析：由AB=0，知rA+rB≤3．又rA＞0，

5.已知向量组α，β，γ线性无关，则k≠1是向量组α+kβ，β+kγ，α—γ线性无关的( )．(C)

A. 充分必要条件

B. 充分条件，但非必要条件

C. 必要条件，但非充分条件

D. 既非充分条件也非必要条件

解析：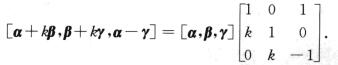

设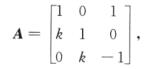

6.设4阶矩阵A=[α_ij]不可逆，且元素α₁₂的代数余子式A₁₂≠0，若矩阵A的列向量组为α₁，

α₂，α₃，α₄，k₁，k₂，k₃为任意常数，则方程组A^*x=0的通解为( )．(C)

A. k₁α₁+k₂α₂+k₃α₃

B. k₁α₁+k₂α₂+k₃α₄

C. k₁α₁+k₂α₃+k₃α₄

D. k₁α₂+k₂α₃+k₃α₄

解析：由于矩阵A不可逆，A₁₂≠0，因此矩阵A的秩为3，故A^*的秩为1，则A^*x=0的通解由3个线性无关的解向量构成．又A^*A=|A|E=0，于是

A^*[α₁，α₂，α₃，α₄]=[A^*α₁，A^*α₂，A^*α₃，A^*α₄]=[0，0，0，0，]

即α_i(i=1，2，3，4)为方程组A^*x=0的解．由A₁₂≠0知，向量组α₁，α₃，α₄线性无关，所以方程组A^*x=0的通解为k₁α₁+k₂α₃+k₃

本文档预览：3000字符，共17856字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载