考研数学三（无穷级数）模拟试卷45
填空题
1.
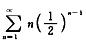
4
解析：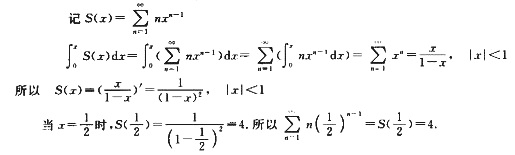
解答题
2.求幂级数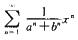
因为
[*]
所以幂級数的收敛半径
[*]
当x＝R，
a≥b时，[*]故级数发散；
a＜b时，[*]发散．
当x＝－R，
a≥b时，[*]
a＜b，[*]
因[*]所以x＝－R时，级数发散.
综上所述，幂级数[*]当a≥b时，收敛域为(－a，a)；当a＜b时，收敛域为(－b，b).
解析：
3.求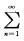
nxn－1的收敛域及和函数，并求级数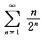
(1)求[*]nxn－1的收敛域.
[*]＝1，收敛半径R＝1，在端点x＝1处，级数为[*]n，发散；在x＝－1处，[*]n(－1)n－1，发散，故收敛域为(－1，1).
(2)求[*]nxn－1的和函数S(x).
设S(x)＝[*]nxn－1，x∈(－1，1)，
[*]
然后两边对x求导，
[*]
(变上限定积分对上限变量求导等于被积函数在上限变量处的函数值)．
下面求[*]的和，因为[*]，x∈(－1，1)，取x＝1／2，则有
[*]
故[*]
解析：
4.求幂级数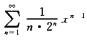
[*]收敛半径R＝1／ρ＝2.
当x＝2时，
[*]
当x＝－2时，
[*]
级数的收敛域为[－2，2).
[*]
两边积分得x．S(x)＝－ln(2－x)＋ln2.
当x≠0时，S(x)＝[*]；
当x＝0时，S(0)＝1／2，所以
[*]
解析：
5.求幂级数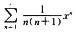
[*]，收敛半径R＝1／ρ＝1.
当x＝－1时，原级数为[*]收敛；当x＝1时，原级数为[*]收敛，故幂级数的收敛域为[－1，1].
[*]
当x＝0时，原级数为[*]＝0收敛.
[*]
当x＝1时，级数为[*]，当x→∞时)；
当x＝－1时，级数为[*]
故[*]的和函数S(x)为[*]
解析：
6.求幂级数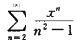
的和函数，并求级数
先求得幂级数的收敛半径为R＝1，收敛区间为(－1，1)，设幂级数的和函数为S(x)，则
[*]
而[*]＝g(x)－x－x2／2＝－ln(1－x)－x－x2／2，
故
[*]
(|x|＜1且x≠0).
当x＝0时，S(x)＝0.令x＝1／2∈(－1，1)，得[*]
解析：
7.求幂级数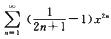
设
[*]
则
S(x)＝S1(x)－S2(x)，x∈(－1，1).
由于
[*]
因此
[*]
又由于S1(0)＝0，故
[*]
所以
[*]
解析：
8.求幂级数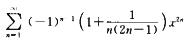
因为
[*]
所以当x2＜1时，原级数绝对收敛；当x＞1时，原级数发散，因此原级数的收敛半径为1，收敛区间为(－1，1).
[*]
由于S(0)＝0，S’(0)＝0，所以
S’(x)＝∫0xS”(t)dt＝∫0x[1／(1＋t2)]dt＝arctanx，S(x)＝∫0xS’(t)dt＝∫0xarctantdt＝xarctanx－ln(1＋x2)／2
又[*]x∈(－1，1)，从而
[*]
解析：
本文档预览：3000字符，共8060字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载