
考研数学三(常微分方程与差分方程)模拟试卷41
填空题
1.微分方程y’+ytanx=cosx的通解为________.
y=(x+C)cosx
解析:由通解公式得
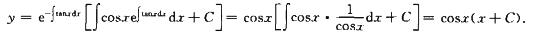
2.微分方程(y+x3)dx-2xdy=0满足y|x=1=6/5的特解为________.
[*]
解析:把原微分方程整理得
y’=y/2x=x2/2.
此方程为一阶线性微分方程.通解为
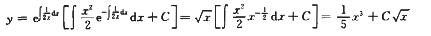
把y|x=1代入通解得C=1.所以特解为
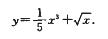
故应填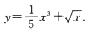
解答题
有一平底容器,其内侧壁是由曲线x=φ(y)(y≥0)绕y轴旋转而成的旋转曲面(如图所示).容器的底而圆的半径为2m,根据设计要求,当以3m3/min的速率向容器内注入液体时,液面的面积将以πm2/min的遠率均匀扩大(能设注入液体前,容器内无液体).(注:m表示长度,单位米:min表示时间.单位分.)
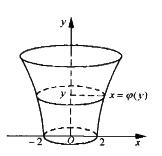
3.根据t时刻液面的面积,写出t与φ(y)之间的关系式;
设在t时刻,液面的高度为y,则由题设知此时液面的面积为
πφ2(y)=4π+πt,
从而t=φ2(y)-4.
解析:
4.求曲线x=φ(y)的方程.
液面的高度为y时,液体的体积为
π∫0yv(u)φ2(u)du=3t=3φ2(y)-12.
上式两边对y求导,得πφ2(y)=6φ(y)φ’(y).即πφ(y)=6φ’(y).
解此微分方程,得φ(y)=Ceπy/6,其中C为任意常数.由φ(0)=2知C=2.故所求曲线方程为x=2eπy/6.
解析:
5.设曲线L的极坐标方帮为r=r(θ),M(r,θ)为L上任一点,M0(2,0)为L上一定点,若极径OM0,OM与曲线L.所围成的曲边扇形面积值等于L上M0、M两点间弧长值的一半,求曲线L的方程.
由已知条件得
[*]
两边对θ求导得[*]
因为[*],所以-arcsin(1/r)+C=±θ.由条件r(0)=2,知C=π/6,
故所求曲线L的方程为
[*]
亦即直线[*]
解析:
6.求微分方程(3x2+2xy-y2)dx+(x2-2xy)dy=0的通解.
令u=y/x,则
[*]
解之得u2-u-1=Cx-3,即y2-xy-x2=Cx-1(或xy2-x2y-x3=C).
解析:
7.求微分方程
令z=y/x,则dy/dx=z+xdz/dx
当x>0时,原方程化为
[*]
其通解为
[*]
代回原变量,得通解y+[*]=C(x>0).
当x<0时,原方程的解与x>0时相同.
解析:
8.求方程x(lnx-lny)dy-ydx=0的通解.
将原方程改写为[*],此为齐次方程.
令u=y/x,则dy/dx=u+xdu/dx,方程化为-lnu(u+xdu/dx)-u=0.
分离变量得[*]
即[*],等式两端积分得lnu-ln(1+lnu)+lnC=-lnx,
从而(1+lnu)/u=Cx.
故所求通解为1+lny-lnx=Cy.
解析:
9.求微分方程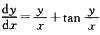
设y/x=u.则dy/dx=xdu/dx+u,原方程变为
xdu/dx+u=u+tanu,即du/dx=tanu/x.
分离变量得cotudu=dx/x,积分得sinu=Cx,故方程通解为sin(y/x)=Cx.
解析:
10.求齐次方程y’=x/y+y/x满足y|x=1=2的特解.
令y/x=u,则原方程变为u+xdu/dx=1/u+u,即udu=dx/x,积分得
u2/2=lnx+C.
将u=y/x代入上式,得通解y2=2x2(lnx+C).
由y|x=1=2知C=2,故特解为
本文档预览:3000字符,共12152字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载