考研数学三（无穷级数）模拟试卷46

考研数学三（无穷级数）模拟试卷46

选择题

1.设函数f(x)是以2π为周期的周期函数，且在闭区间[－π，π]上有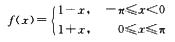(A)

A. 1＋π

B. 1－π

C. 1

D. 0

解析：因为f(－π)＝1－(－π)＝1＋π，f(π)＝1＋π.所以f(x)的傅立叶级数在x＝π处收敛于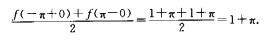

2.设f(x)＝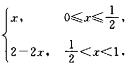

S(x)＝a₀／2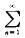＋(C)

A. 1／2

B. －1／2

C. 3／4

D. －3／4

解析：本题把f(x)进行偶延拓，展为余弦级数，由于x＝－5／2为f(x)延拓后所得函数的间断点，故根据狄立克菜充分条件

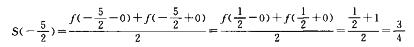
3.若级数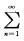a_n收敛，则________．

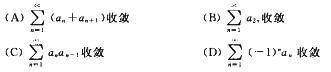(A)

A.

B.

C.

D.

解析：由级数基本性质知，若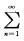a_n收敛，则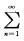a_n＋1也收敛，故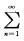

4.设有以下命题:

(B)

A. ①②

B. ②③

C. ③④

D. ④①

解析：①是错误的，如令u_n＝(－1)ⁿ，显然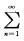u_n发散，而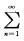(u_n＋1＋u_2n)收敛.

②是正确的，因为改变(增加或减少)级数的有限项，不改变级数的收敛性.

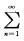③是正确的，因为由可得到u_n不趋于零(n→∞)，所以u_n发散.

④是错误的，如令u_n＝1／n，v_n＝－1／n，显然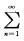u_n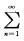，v_n都发散，而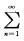

填空题

5.设函数f(x)＝πx＋x²(－π＜x＜π)的傅立叶级数服开式为

2π／3

解析：b₃＝(1／π)∫_－π^π(πx＋x²)sin3xdx＝(2／π)∫₀^ππxsin3xdx

＝(－2／3)xcos3x｜₀^π＋(2／3)∫₀^πcos3xdx＝2π／3＋(2sin3x／9)｜₀^π＝2π／3．

故应填2π／3．

6.设f(x)是可积函数.且在[－π，π]上恒有f(x＋π)＝f(x)，则a_2n－1＝________．

0，0

解析：a_n＝(1／π)f(x)cosnxdx＝(1／π)∫_－π⁰f(x)cosnxdx＋(1／π)∫₀^πf(x)cosnxdx

∫₀本文档预览：3000字符，共10124字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载