考研数学一（高等数学）模拟试卷435

考研数学一（高等数学）模拟试卷435

选择题

1.设f(x)是二阶常系数非齐次线性微分方程y’’+py’+qy=sin 2x+2e^x的满足初始条件f(0)=f’(0)=0的特解，则当x→0时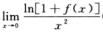，(C)

A. 不存在

B. 等于0

C. 等于1

D. 其他

解析：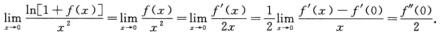

将f(0)=f’(0)=0代入原微分方程，解得f’’(0)=2，于是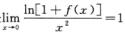

2.设f(x)为单调可微函数，g(x)与f(x)互为反函数，且f(2)=4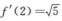，(B)

A. 1／4

B. 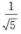C. 1／6

D. 4

解析：由g(x)与f(x)互为反函数，得g[f(x)]=x．

上式对x求导得g’[f(x)]·f’(x)=1．

由f(2)=4得g’(4)·f’(2)=1，即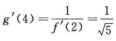

3.设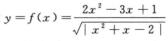(C)

A. 两条铅直渐近线，两条斜渐近线

B. 两条铅直渐近线，一条斜渐近线

C. 一条铅直渐近线，两条斜渐近线

D. 一条铅直渐近线，一条斜渐近线

解析：由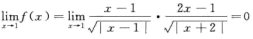得x=1不是曲线的铅直渐近线；

由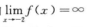得x=-2为曲线的铅直渐近线；

由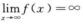得曲线y=f(x)没有水平渐近线；

由

得y=-2x+4为曲线的斜渐近线；

由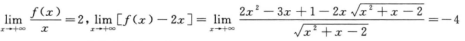

4.设y(x)是微分方程y’’+(x-1)y’+x²y=e^x满足初始条件y(0)=0，y’(0)=1的解，则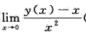(A)

A. 等于1

B. 等于2

C. 等于0

D. 不存在

解析：微分方程y’’+(x-1)y’+x²y=e^x中，令x=0，则y’’(0)=2．

于是

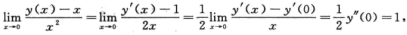
填空题

5.

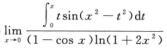
1／4．

解析：由∫₀^xtsin(x²-t²)dt=-1／2∫₀^xsin(x²-t²)d(x²-t²)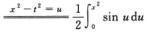得

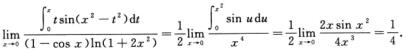
6.当x→0时，(1+ax²)^1／3-1～cos²x-1，则a=________．

-3．

解析：因为当x→0时，

(1+ax²)^1／3-1～a／3x²，cos²x-1=(cos x+1)(cos x-1)～-x²，且(1+ax²)^1／3-1～cos²x-1，所以a=-3．

7.设F(x)=∫₀^x(x²-t²)f’(t)dt，其中f’(x)在x=0处连续，且当x→0时，F’(x)～x²，则f’(0)=________．

1／2．

解析：F(

本文档预览：3000字符，共15337字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载