
考研数学一(高等数学)模拟试卷428
选择题
1.设α=(1+x)sin 2x-1,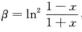 (C)
(C)
A. α是β的高阶无穷小
B. α是β的低阶无穷小
C. α是β的同阶非等价的无穷小
D. α是β的等价无穷小
解析:当x→0时,α=(1+x)sin 2x-1=esin 2x·ln(1+x)-1~sin 2x·ln(1+x)~2x2,
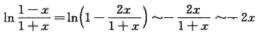 ,则
,则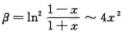
2.设f(x)连续且f(x)在x=a处可导,若g(x)=|f(x)|在x=a处不可导,则( ).(C)
A. f(a)≠0,f’(a)=0
B. f(a)≠0,f’(a)≠0
C. f(a)=0,f’(a)≠0
D. f(a)=0,f’(a)=0
解析:当f(a)≠0时,若f(a)>0,则在x=a的邻域内|f(x)|=f(x);若f(a)<0,则在x=a的邻域内|f(x)|=-f(x),显然|f(x)|在x=a处可导,故若|f(x)|在x=a处不可导,则f(a)=0;
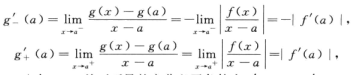
3.设f(x)二阶连续可导,且 (C)
(C)
A. f(0)是f(x)的极小值
B. f(0)是f(x)的极大值
C. (0,f(0))是曲线y=f(x)的拐点
D. x=0是f(x)的驻点但不是极值点
解析:因为f(x)二阶连续可导,且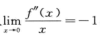 ,所以
,所以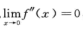 ,即f’’(0)=0.又
,即f’’(0)=0.又
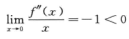
4.设f(x)在R上是以R为周期的连续奇函数,则下列函数中不是周期函数的是( ).(D)
A. ∫0xf(t)dt
B. ∫-xaf(t)dt
C. ∫-x0f(t)dt-∫x0f(t)dt
D. ∫-xxtf(t)dt
解析:设φ(x)=∫-xxtf(t)dt=2∫0xtf(t)dt.
φ(x+T)=2∫0x+Ttf(t)dt=2∫0xtf(t)dt+2∫xx+Ttf(t)dt≠φ(x),选D.
5.设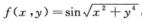 (C)
(C)
A. f’x(0,0),f’y(0,0)都不存在
B. f’x(0,0)存在,f’y(0,o)不存在
C. f’x(0,0)不存在,f’y(0,o)存在
D. f’x(0,0),f’y(0,0)都存在
解析:因为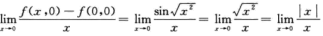 不存在,所以f’x(0,0)不存在;
不存在,所以f’x(0,0)不存在;
由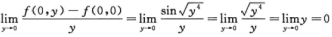
6.设积分区域为D={(x,y)|1/2≤x+y≤1,x≥0,y≥0},
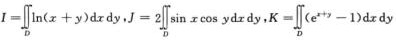 (D)
(D)
A. K<I<J
B. J<I<K
C. I<K<J
D. I<J<K
解析:当(x,y)∈D时,ln(x+y)≤0,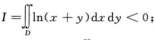
因为区域D关于y=x对称,所以 ,于是
,于是
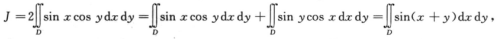
7.设Ω为由