考研数学二（常微分方程）模拟试卷34

考研数学二（常微分方程）模拟试卷34

选择题

1.微分方程y”－y＝e^x＋1的一个特解应具有形式(式中a.b为常数)________．(B)

A. ae^x＋b

B. axe^x＋b

C. ae^x＋bx

D. axe^x＋bx

解析：将A、B、C、D各选项表示的函数直接代入方程知B为正确选项.当然也可以用下面的方法来选择:

方程y”－y＝e^x＋1对应的齐次方程的特征方程是r²－1＝0

因此1是特征方程的根，而0不是特征方程的根，从面由线性微分方程解的结构和求特解的待定系数法知B是正确选项.

2.微分方程y”＋y＝x²＋1＋sinx的特解形式可设为(A)

A. y^*＝ax²＋bx＋c＋x(Asinx＋Bcosx)

B. y^*＝x(ax²＋bx＋c＋Asinx＋Bcosx)

C. y^*＝ax²＋bx＋c＋Asinx

D. y^*＝ax²＋brx＋c＋Acosx

解析：微分方程的特征方程为r²＋1＝0，特征根为r＝±i，y”＋y＝x²＋1的特解形式为

y₁^*＝ax²＋bx＋c，

y”＋y＝sinx的特解形式为

y₂^*＝x(Asinx＋Bcosx)，

故所求微分方程的特解形式为

y^*＝y₁^*＋y₂^*＝ax²＋bx＋c＋x(Asinx＋Bcosx).

故应选A.

3.函数y＝C₁e^x＋C₂e^－x＋xe^x满足的一个微分方程是________．(D)

A. y”－y’－2y＝3xe^x

B. y”－y’－2y＝3e^x

C. y”＋y’－2y＝3xe^x

D. y”＋y’－2y＝3e^x

解析：特征方程两根为r₁＝1，r₂＝－2，特征方程为(r－1)(r＋2)＝0，r²＋r－2＝0排除选项A、B.

由y＝xe^x，y’＝(1＋x)e^x.y”＝(2＋x)e^x代入方程

y”＋y’－2y＝(2＋x)e^x＋(1＋x)e^x－2xe^x＝3e^x.

故应选D.

4.具有特解y₁＝e^－x，y₂＝2xe^－x，y₃＝3e^x的3阶常系数齐次线性微分方程是________.(B)

A. y’’’－y”－y’＋y＝0

B. y’’’＋y”－y’－y＝0

C. y’’’－6y”＋11y’－6y＝0

D. y’’’－2y”－y’＋2y＝0

解析：由三个特解形式知此微分方程特征根为r₁＝r₂＝－1，r₃＝1，故特征方程应为:

(r＋1)²(r－1)＝0，r³＋r²－r－1＝0，

所以微分方程应为y’’’＋y”－y’－y＝0.

故应选B.

5.设y＝y(x)是二阶常系数微分方程y”＋py’＋qy＝e^3x满足初始条件y(0)＝y’(0)＝0的特解，则当x→0时，函数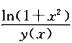(C)

A. 不存在

B. 等于1

C. 等于2

D. 等于3

解析：由y＝y(x)为微分方程特解知y”(x)＝e^3x－py’(x)－qy(x).

由洛必达法则

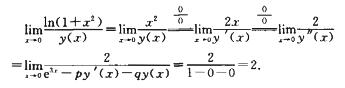
填空题

6.设y＝e^x(C₁sinx＋C₂cosx)(C₁，C₂为任意常数)为某二阶常系数线性齐次微分方程的通解，则该方程为________．

y”－2y’＋2y＝0

解析：由通解形式知该微分方程的特征根为r＝1±i，从而特征方程为r²－2r＋2＝0，微分方程应为y”－2y’＋2y＝0..

故应填y”－2y’＋2y＝0.

7.y”－4y＝e^2x的通解为________．

y＝C₁e^－2x＋(C₂＋x／4)e^2x

解析：对应齐次方程的特征方程为r²－4＝0，特征根为r＝±2，故齐次方程通解为

Y＝C₁e^－2x＋C₂e^2x.

设原方程特解为y^*＝Axe^2x，代入原方程可得A＝1／4，因此，原方程的通解为

y＝C₁e^{－2x本文档预览：3000字符，共12288字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}