考研数学一（高等数学）模拟试卷422

考研数学一（高等数学）模拟试卷422

选择题

1.设{a_n}与{b_n}为两个数列，下列说法正确的是( )．

D

解析：A不正确，例如：a_n=2+(-1)ⁿ，b_n=2-(-1)ⁿ，显然{aⁿ}与{bⁿ}都发散，但aⁿbⁿ=3，显然{aⁿbⁿ}收敛；B、C都不正确，例如：aⁿ=n[1+(-1)ⁿ]，bⁿ=n[1-(-1)ⁿ]，显然{aⁿ}与{bⁿ}都无界，但aⁿbⁿ=0，显然{aⁿbⁿ}有界且

2.设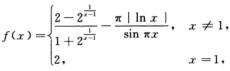(C)

A. 连续点

B. 可去间断点

C. 跳跃间断点

D. 第二类间断点

解析：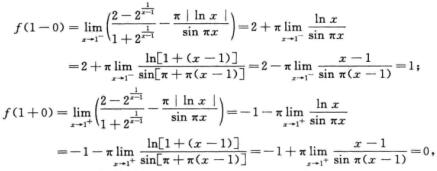

3.下列说法中正确的是( )．(D)

A. 若f’(x₀)＜0，则f(x)在x₀的邻域内单调递减

B. 若f(x)在x₀取极大值，则当x∈(x₀-δ，x₀)时，f(x)单调递增，当x∈(x₀，x₀+δ)时，f(x)单调递减

C. f(x)在x₀取极值，则f(x)在x₀连续

D. f(x)为偶函数，f’’(0)≠0，则f(x)在x=0处一定取到极值

解析：设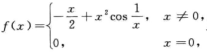则有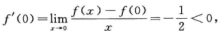

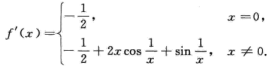
当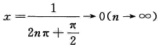时，f’(x)=1／2＞0，则f(x)在x=0的任意邻域内都不单调递减，A不正确；

设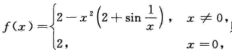则f(x)在x=0处取得极大值，但其在x=0的任意邻域内皆不单调，B不正确；

设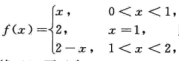

4.设函数f(x)连续，F(x)为f(x)的一个原函数，下列正确的是( )．(B)

A. 若f(x)为偶函数，则F(x)为奇函数

B. 若f(x)为奇函数，则F(x)为偶函数

C. 若f(x)为增函数，则F(x)为增函数

D. 若f(x)为周期函数，则F(x)为周期函数

解析：方法一 f(x)=cos x为偶函数，F(x)=sin x+2为f(x)的一个非奇非偶的原函数；

f(x)=x为单调增函数，F(x)=1／2x²为f(x)的一个非单调递增的原函数；

f(x)=cos x-1是周期为2π的函数，F(x)=sin x-x为f(x)的非周期原函数，选B．

方法二 设f(-x)=-f(x)，F(x)=∫_a^xf(t)dt为f(x)的一个原函数．

由F(-x)=∫_a^-xf(t)dt

填空题

5.设f’(x)连续可导，且f(0)=0，f’(0)=1，则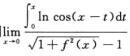

0．

解析：当x→0时，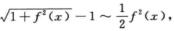

∫₀^xln cos(x-t)dt=-∫₀^xln cos(x-t)d(x-t)

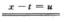-∫_x⁰ln cos udu=∫₀^xln xos udu，

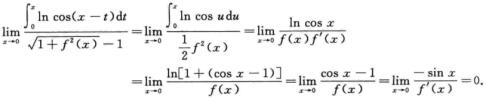
6.设本文档预览：3000字符，共14564字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载