考研数学一（概率统计）模拟试卷49

考研数学一（概率统计）模拟试卷49

选择题

1.设连续型随机变量X的密度函数为f(x)，分布函数为F(x)．如果随机变量X与-X分布函数相同，则( )．(C)

A. F(x)=F(-x)

B. F(x)=-F(-x)

C. f(x)=f(-x)

D. f(x)=-f(-x)

解析：F_X(x)=P(X≤x)=∫_-∞^xf(t)dt；

F_-X(x)=P(-X≤x)=P(X≥-x)=1-P(X≤-x)=1-∫_-∞^-xf(t)dt．

因为X与-X有相同的分布函数，所以∫_-∞^xf(t)dt=1-∫_-∞^-xf(t)dt，两边求导数，得f(x)=f(-x)，选C．

2.设随机变量X～U[1，7]，则方程x²+2Xx+9=0有实根的概率为( )．(C)

A. 1／2

B. 1／3

C. 2／3

D. 0

解析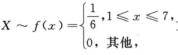：方程x²+2Xx+9=0有实根的充要条件为

△=4X²-36≥0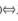

3.设随机变量X，Y相互独立，X～U(0，2)，Y～E(1)，则P(X+Y＞1)等于( )．(A)

A. 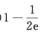B. 1-e

C. e

D. 2e

解析：由X～U(0，2)，Y～E(1)得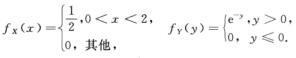

再由X，Y相互独立得(X，Y)的联合密度函数为

得

=1-1／2∫₀¹dx∫₀^1-xe^-ydy=1-1／2∫₀¹(1-e^x-1)dx

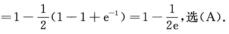
4.设(X，Y)服从二维正态分布，则下列说法不正确的是( )．(A)

A. X，Y一定相互独立

B. X，Y的任意线性组合l₁X+l₂Y(l₁，l₂不全为零)服从正态分布

C. X，Y都服从正态分布

D. ρ=0时X，Y相互独立

解析：因为(X，Y)服从二维正态分布，所以B、C、D都是正确的，只有当ρ=0时，X，Y才相互独立，所以选A．

5.设X，Y为两个随机变量，若E(XY)=E(X)E(Y)，则( )．(B)

A. D(XY)=D(X)D(Y)

B. D(X+Y)=D(X)+D(Y)

C. X，Y独立

D. X，Y不独立

解析：因为E(XY)=E(X)E(Y)，所以Cov(X，Y)=0．

又D(X+Y)=D(X)+D(Y)+2Cov(X，Y)，所以D(X+Y)=D(X)+D(Y)，选B．

6.设X～t(2)，则1／X²服从的分布为( )．(C)

A. χ²(2)

B. F(1，2)

C. F(2，1)

D. χ²(4)

解析：因为X～t(2)，所以存在U～N(0，1)，V～χ²(2)，又因为U，V相互独立，使得

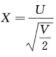，则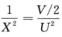

7.在假设检验中，H₀为原假设，下列选项中犯第一类错误(弃真)的是( )．(B)

A. H₀为假，接受H₀

B. H₀为真，拒绝H₀

C. H₀为假，拒绝H₀

D. H₀为真，接受H₀

解析：

填空题

8.设P(B)=0．5，P(A-B)=0．3，则P(A+B)=________．

0．8．

解析：因为P(A-B)=P(A)-P(AB)，所以P(A+B)=P(A-B)+P(B)=0．8．

9.设事件A，B，C两两独立，满足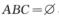

1／4．

解析：由P(A+B+C)=P(A)+P(B)+P(C)-P

本文档预览：3000字符，共9318字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载