考研数学一（填空题）模拟试卷65

考研数学一（填空题）模拟试卷65

填空题

1.设10件产品中有4件不合格品，从中任取2件，已知所取的两件中有一件是不合格品，则另一件也是不合格品的概率为_______．

[*]

解析：记A={取的2件产品中至少有1件是不合格品)，B={取的2件产品都是不合格品)，则P(A)=，有AB=B，所求概率为P(B|A)=

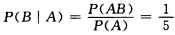
2.

[*]

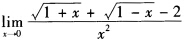
解析：将分子化简后，应用等价无穷小因子代换．易知

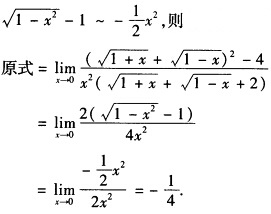
3.已知L是第一象限中从点(0，0)沿圆周x²+y²=2x到点(2，0)，再沿圆周x²+y²=4到点(0，2)的曲线段．计算曲线积分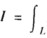

(π/2)-4

解析：

4.设K，L，δ为正的常数，则[δK^－x+(1－δ)L^－x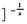

K^δL^1－δ

解析：属1^∞型极限．原式=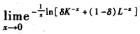，而

5.设两曲线y=x²+ax+b与一2y=一1+xy³在点(一1，1)处相切，则a=___________，b=___________。

3，3

解析：因为两曲线过点(一1，1)，所以b一a=0，又由y=x²+ax+b得

6.设A，B，C均为n阶矩阵，E为n阶单位矩阵，若B=E+AB，C=A+CA，则B-C为_____.

E

解析：由B=E+AB (E-A)B=E B=(E-A)^-1．

由C=A+CA C(E-A)=A C=A(E-A)^-1．

B-C=(E-A)^-1-A(E-A)^-1=(E-A)(E-A)^-1=E．

7.

[*]

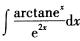
解析：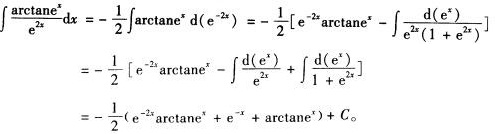

8.设f(x)是以T为周期的连续函数，且F(x)=∫₀^xf(t)dt+bx也是以T为周期的连续函数，则b=_________．

[*]∫₀^Tf(t)dt

解析：F(x+T)=∫₀^x＋Tf(t)dt+b(x+T)=∫₀^xf(t)dt+bx+∫_x^x＋Tf(t)dt+bT=F(x)+∫_x^x＋Tf(t)dt＋bT=F(x)+∫₀^Tf(t)dt＋bT，由F(x+T)=F(x)，得b=

9.已知f(x)=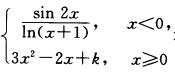

2

解析：因为f(x)在x=0处连续，所以=f(0)．而

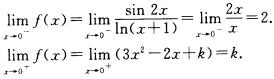
10.设f(χ₁，χ₂)＝

[*]

解析：把行列式展开就可以得到二次型的一般表达式．

因此对应的矩阵为本文档预览：3000字符，共9015字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载