2019年上半年中学教师资格认定考试（高级数学学科知识与教学能力）真题试卷
单项选择题
1.下列选项中，运算结果一定是无理数的是( )。(A)
A. 有理数与无理数的和
B. 有理数与有理数的差
C. 无理数与无理数的和
D. 无理数与无理数的差
解析：本题考查有理数与无理数的性质。(1)有理数与有理数：和、差、积、商均为有理数(求商时分母不为零)。(2)有理数与无理数：①一个有理数和一个无理数的和、差为无理数；②一个非零有理数与一个无理数的积、商为无理数。(3)无理数与无理数：和、差、积、商可能是有理数，也可能是无理数。故本题选A。
2.在空间直角坐标系中，由参数方程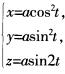
(0≤t≤2π)所确定的曲线的一般方程是( )。
(B)
A.
B.
C.
D.
解析：本题考查空间曲线的方程。由
，可得x+y=acos2t+asin2t=a，z2=a2(2sintcost)2=4xy，所以将参数方程化成一般方程为
3.已知空间直角坐标与球坐标的变换公式为
(ρ≥0，－π＜φ≤π，
)，则在球坐标系中，θ=
(D)
A. 柱面
B. 圆面
C. 半平面
D. 半锥面
解析：本题考查直角坐标与球坐标变换、空间曲面方程。
设球坐标中任意一点P(ρ，θ，φ)，根据题目中空间直角坐标与球坐标的变换公式可知，ρ表示原点O与点P之间的径向距离，θ表示OP′到OP的有向角，其中OP′是OP在xOy。坐标面上的投影，φ表示Ox轴到OP’的有向角，如图1所示。因此，θ=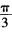
表示以原点为顶点，以射线OP为母线，以z轴为中心轴的半锥面，如图2所示。故本题选D。
4.设A为n阶方阵，B是A经过若干次初等行变换得到的矩阵，则下列结论正确的是( )。(C)
A. ｜A｜=｜B｜
B. ｜A｜≠｜B｜
C. 若｜A｜=0，则一定有｜B｜=0
D. 若｜A｜＞0，则一定有｜B｜＞0
解析：本题考查矩阵初等变换及行列式的性质。对矩阵可以作如下三种初等行(列)变换：①交换矩阵的两行(列)；②将一个非零数k乘到矩阵的某一行(列)；③将矩阵的某一行(列)的k倍加到另一行(列)上。若方阵A，经过以上三种初等变换得到方阵B，则对应的行列式的关系依次为｜A｜=－｜B｜，｜A｜=k｜B｜，｜A｜=｜B｜。即｜A｜=a｜B｜，a∈R。所以｜A｜=0时必有｜B｜=0。故本题选C。
5.已知f(x)=
(B)
A. －1
B. 0
C. 1
D. π
解析：本题考查泰勒展式的相关知识。因为sinx=
6.若矩阵A=
(C)
A. x=－2，y=2
B. x=1，y=－1
C. x=2，y=－2
D. x=－1，y=1
解析：本题考查矩阵的相似对角化的相关知识。由题意可知，矩阵A可以相似对角化，且λ=2对应两个线性无关的特征向量，所以(2E－A)x=0有两个线性无关的解，即有3－r(2E－A)=2，所以r(2E－A)=1。2E－A=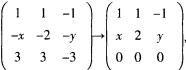
，要使r(2E－A)=1，则有
7.下列表述属于数学直观想象素养的是( )。
①利用图形描述，分析数学问题；
②借助空间形式认识事物的位置关系，形态变化和运动规律；
③建立形与数的关系，构建数学问题直观模型，探索解决问题的思路；
④在实际情境中从数学的视角发现问题，提出问题，分析问题，建立模型。(A)<
本文档预览：3000字符，共11639字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
