考研数学三（概率论与数理统计）模拟试卷104

考研数学三（概率论与数理统计）模拟试卷104

选择题

1.设随机变量X的分布函数F(x)=则P{X=1}=

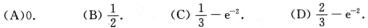(D)

A.

B.

C.

D.

解析：本题：考查如何利用分布函数来计算随机变量取值的概率，属基本题．根据分布函数的性质，有

P{X=1}=P{X≤1}－P{X＜1}=F(1)－F(1－0)=1－e^-2－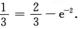

2.设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=1／2，记F_Z(z)为随机变量Z=XY的分布函数，则函数F_Z(z)的间断点个数为(B)

A. 0

B. 1

C. 2

D. 3

解析：根据分布函数的定义，有

F_Z(z)=P{XY≤z}=P{Y=0}P{XY≤z｜Y=0}+P{Y=1}P(XY≤z｜Y=1}

=1／2[P{XY≤z｜Y=0}+P{XY≤z｜Y=1}]

=1／2[P{X·0≤z｜Y=0}+P{X≤z｜Y=1}]．

因为X与Y相互独立，所以

F_Z(z)=1／2[P{X·0≤z}+P{X≤z}]．

当z＜0时，F_Z(z)=1／2φ(z)；

当z≥0时，F_Z(z)=1／2[1+φ(z)]．

可见z=0为间断点，故应选(B)．

3.设X～N(μ，σ²)，F(x)为其分布函数，μ＜0，则对于任意实数a，有(A)

A. F(-a)+F(a)＞1

B. F(-a)+F(a)=1

C. F(-a)+F(a)＜1

D. F(μ－a)+F(μ+a)=1＜2

解析：利用标准正态分布的性质，有

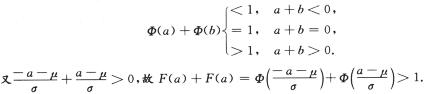
4.设随机变量X与Y相互独立，且E(X)与E(Y)存在，记U=max{X，Y}，V=min{X，Y)，则E(UV)=(B)

A. E(U)E(V)

B. E(X)E(Y)

C. E(U)E(Y)

D. E(X)E(V)

解析：因为U=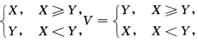

5.设X₁，X₂，X₃为来自正态总体N(0，σ²)的简单随机样本，则统计量S=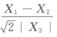(C)

A. F(1，1)

B. F(2，1)

C. t(1)

D. t(2)

解析：因为X₁-X₂～N(0，2σ²)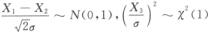，，而且X₁，X₂，X₃相互独立，故随机变量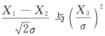相互独立．

由t分布的定义知统计量S=

填空题

6.4重伯努利试验中，已知“成功”的概率为1／2，则在没有出现全部“失败”的情况下，“成功”不止一次的概率为________．

[*]

解析：设X表示4重伯努利试验中“成功”的次数，则X～B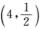，于是所求概率为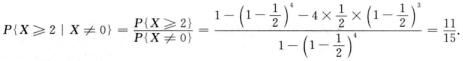

7.设随机变量X服从参数为1的泊松分布，则P{X=E(X²)}=________．

[*]

解析：此题虽然只是计算概率，但首先要算E(X²)=D(X)+[E(X)]²，利用指数分布的数字特征．

由X服从参数为1的泊松分布知E(X)=D(X)=1，

因此E(X²)=D(X)+[E(X)]²=2．

所以P{X=E(X²))=P{X=2}=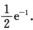，故应填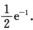

8.设X的密度函数f(x)=本文档预览：3000字符，共8998字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载