考研数学三（线性代数）模拟试卷186

考研数学三（线性代数）模拟试卷186

选择题

1.已知向量组α₁=(1，-1，2，-4)^T，α₂=(1，1，a，4)^T，α₃=(-1，a，1，a²)^T线性相关，则(C)

A. a=0

B. a=-1

C. a=4

D. a=2

解析：s个n维向量α₁，α₂，…，α_s线性相关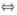秩r(α₁，α₂，…，α_s)＜s

r(α₁，α₂，α₃)＜3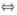

2.和矩阵A=相似的是

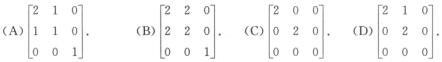(C)

A.

B.

C.

D.

解析：

矩阵

填空题

3.已知A，B均为3阶矩阵．｜A｜=3，｜B｜=2，｜A+B｜=24，则｜A^-1+B^-1｜=________．

4

解析：A^-1+B^-1=EA^-1+B^-1E=(B^-1B)A^-1+B^-1(AA^-1)

=B^-1(B+A)A^-1

所以｜A^-1+B^-1｜=｜B^-1｜·｜B+A｜·｜A^-1｜=｜B｜^-1·｜A+B｜·｜A｜^-1=4．

4.已知A，B均为3阶矩阵，且｜A｜=2，｜B｜=-1，C=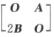

[*]

解析：由拉普拉斯展开式，得

｜C｜=(-1)^3×3｜A｜｜2B｜=16，

那么C^*=｜C｜C^-1=16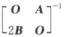，而C^-1可以用分块矩阵的初等行变换来完成，即

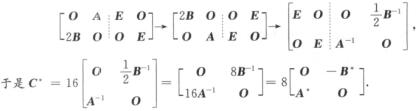
当然，直接用公式

5.已知α₁=(-3，2，0)^T，α₂=(-1，0，-2)^T是方程组

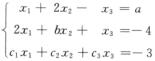
(-3，2，0)^T+k(-1，1，1)^T

解析：方程组系数矩阵A中有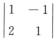

6.已知向量β=(0，2，-1，a)^T可以由α₁=(1，-2，3，-4)^T，α₂=(0，1，-1，1)^T，α₃=(1，3，a－3，1)^T线性表出，则a=________．

设x₁α₁+x₂α₂+x₃α₃=β，

对(α₁，α₂，α₃，β)作初等行变换，有

[*]

所以a=2时向量β可由α₁，α₂，α₃线性表出．

解析：

7.已知

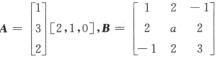
12

解析：AB－2B=(A－2E)B

本文档预览：3000字符，共12241字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载