考研数学三（线性代数）模拟试卷185

考研数学三（线性代数）模拟试卷185

选择题

1.设α₁=(1，0，2，3)^T，α₂=(1，1，3，5)^T，α₃=(1，-1，a+2，1)^T，α₄=(1，2，4，a+5)^T，那么a=2是向量组α₁，α₂，α₃，α₄线性相关的(B)

A. 充分必要条件

B. 充分而非必要条件

C. 必要而非充分条件

D. 既不充分也不必要条件

解析：n个n维向量α₁，α₂，…，α_n线性相关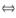｜α₁，α₂，…，α_n｜=0

由｜α₁，α₂，α₃，α₄｜=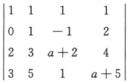

2.设A=(α₁，α₂，α₃，α₄)是4阶矩阵，齐次方程组Ax=0的通解是k(0，1，2，3)^T，则下列命题

①α₂，α₃必线性无关；

②α₁，α₂，α₃必线性无关；

③α₂，α₃，α₄必线性相关．

正确的一共有(A)

A. 3个

B. 2个．

C. 1个

D. 0个

解析：由解的结构，知r(α₁，α₂，α₃，α₄)=3．

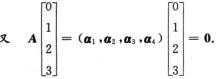
即 α₂+2α₃+3α₄=0．

故α₂，α₃，α₄必线性相关．③正确．

若α₂，α₃线性相关，不妨设α₂=kα₃，则α₄=-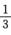

填空题

3.A是n阶实对称矩阵且A²+2A=O，如秩r(A)=r，则｜A+3E｜=________．

3^n－r

解析：设Aα=λα，α≠0，则A²α=λ²α．

由A²+2A=O有(λ²+2λ)α=0．

于是λ=0或-2．

因A是实对称矩阵，必有A～A，且

r(A)=r(A)=r．

从而λ=-2是A的r重特征值，λ=0是A的n－r重特征值．

那么A+3E的特征值：1(r重)，3(n－r重)，

所以｜A+3E设=3^n－r．

4.已知α=(1，3，2)^T，β=(1，-1，2)^T，B=αβ^T．若A和B相似，则(2A+E)^*的特征值为________．

1，5，5

解析：r(B)=r(αβ^T)=1，α^Tβ=2，

知B的特征值：2，0，0，

那么2A+E的特征值：5，1，1．

又｜2A+E｜=5×1×1=5，

故(2A+E)^*的特征值：1，5，5．

5.设矩阵A的伴随矩阵A^*=

[*]

解析：由｜A｜³=｜A^*｜==8，知｜A｜=2．

由(kA)^*=k^n－1A^*知(2A^-1)^*=2³(A^-1)^*=8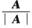=4A，

故矩阵方程为

4ABA^*=4AB+16A

即有B(A^*－E)=4E，

B=4(A^*－E)^-1=

6.已知A=本文档预览：3000字符，共14866字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载