考研数学三（线性代数）模拟试卷188

考研数学三（线性代数）模拟试卷188

选择题

1.设α₁=(A)

A. α₁，α₂，α₃必线性无关

B. α₂，α₃，α₄必线性相关

C. α₁，α₂，α₃，α₄必线性无关

D. α₁，α₂，α₃，α₄必线性相关．

解析：如果C正确，则A必正确．所以C必错误．

如果B正确，则D必正确．所以B必错误．

由

2.已知A=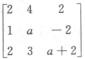(B)

A. a=1时必有｜B｜=0．

B. a=-1时必有｜B｜=0．

C. a=3时必有｜B｜≠0．

D. a=-3时必有｜B｜≠0．

解析：由AB=O有r(A)+r(B)≤3，

又A，B均为非零矩阵，r(A)≥1，r(B)≥1，那么1≤r(B)≤2．

故对任意的a，有｜B｜=0．因此应排除(C)(D)．

而当a=1时，

｜A｜=

3.三知向量组α₁，α₂，α₃的秩r(α₁，α₂，α₃)=3，则向量组aα₁+α₂，aα₂+α₃，aα₃+α₁的秩等于3的充分必要条件是(D)

A. a=1．

B. a=-1．

C. a≠1．

D. a≠-1．

解析：记β₁=aα₁+α₂，β₂=aα₂+α₃，β₃=aα₃+α₁，则

(β₁，β₂，β₃)=(α₁，α₂，α₃)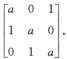

由r(α₁，α₂，α₃)=3，故

r(β₁，β₂，β₃)=3

4.已知P^-1AP=(A)

A. ①②

B. ①④

C. ②③

D. ③④

解析：α₁，α₂是不同特征值的特征向量，那么α₁+α₂不是矩阵A的特征向量，③不正确．④中特征向量与A中特征值错位，故④不正确．

所以应选(A)．

5.二次型x^TAx=x₁²+3x₂²－2x₃²+4x₁x₃的标准形可以是(B)

A. y₁²+3y₂²+5y₃²

B. y₁²+2y₂²－3y₃²

C. y₁²－2y₂²－6y₃²

D. 3y₂²－5y₃²

解析：标准形由p，q决定，标准形是不唯一的．由配方法有

x^TAx=(x₁²+4x₁x₃+4x₃²)+3x₂²－6x₃²

=(x₁+2x₃)²+3x₂²－6x₃²，

p=2，q=1，

故应选(B)．

6.和矩阵A=本文档预览：3000字符，共14994字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载