考研数学三（线性代数）模拟试卷175

考研数学三（线性代数）模拟试卷175

选择题

1.设A，B是三阶方阵，且|A|=1，|B|=－2，则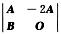(D)

A. 4．

B. －4．

C. 16．

D. －16．

解析：由拉普拉斯展开式，得

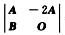
2.三阶矩阵A可逆，把矩阵A的第2行与第3行互换得到矩阵B，把矩阵B的第1列的－3倍加到第2列得到单位矩阵E，则A^*=

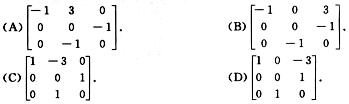(B)

A.

B.

C.

D.

解析：据已知条件P₁A=B，其中P₁=；BP₂=E，其中

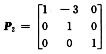
于是

P₁AP₂=E．

故

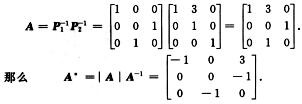
3.设A=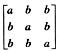(C)

A. a=b或a+2b=0．

B. a=b或a+2b≠0．

C. a≠b且a+2b=0．

D. a≠b且a+2b≠0．

解析：由伴随矩阵A^*秩的公式

若a=b，易见r(A)≤1，可排除(A)和(B)．

当a≠b时，A中有2阶子式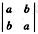≠0，从而r(A)=2|A|=0．而

|A|=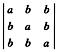

4.设α₁，α₂，α₃，α₄是三维非零向量，则下列命题中正确的是(C)

A. 若α₁，α₂线性相关，α₃，α₄线性相关，则α₁+α₃，α₂+α₄必线性相关．

B. 若α₁，α₂，α₃线性无关，则α₁+α₄，α₂+α₄，α₃+α₄必线性无关．

C. 若α₄不能由α₁，α₂，α₃线性表示，则α₁，α₂，α₃必线性相关．

D. 若α₄能由α₁，α₂，α₃线性表示，则α₁，α₂，α₃必线性无关．

解析：因为α₁，α₂，α₃，α₄是4个3维向量，所以知α₁，α₂，α₃，α₄一定线性相关．

若α₁，α₂，α₃线性无关，而α₁，α₂，α₃，α₄线性相关，则α₄必可由α₁，α₂，α₃线性表示．现(C)中α₄不能由α₁，α₂，α₃线性表示，那么α₁，α₂，α₃肯定线性相关，故(C)一定成立．

而当α₄可由α₁，α₂，α₃线性表出时，α₁，α₂，α₃既可能线性相关，也可能线性无关，故(D)不正确．例如

α₁=(1，0，0)^T，α₂=(0，1，0)^T，α₃=(2，0，0)^T，α₄=(1，1，0)^T，

有α₄=α₁+α₂本文档预览：3000字符，共16391字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载