考研数学三（微积分）模拟试卷285

考研数学三（微积分）模拟试卷285

选择题

1.设α₁=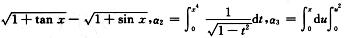(A)

A. α₁，α₂，α₃．

B. α₁，α₃，α₂．

C. α₂，α₁，α₃．

D. α₃，α₁，α₂．

解析：

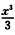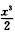又因为tan x=x++o(x³)，sin x=x－+o(x³)，所以tan x－sin x=+o(x³)，tan x－sin x与x³同阶，从而α₁与x³同阶．

由于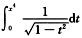=arcsin x⁴，而当x→0时，arcsin x⁴～x⁴，故α₂与x⁴同阶．

记F(x)=∫₀^xdu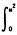arctan tdt，则F′(x)=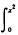

2.设f(x)是以4为周期的连续函数，且f′(1)=－1，F(x)=∫₀^xf(t)dt，则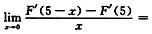(D)

A. 1/2．

B. 0．

C. －1．

D. 1．

解析：由题设知F′(x)是以4为周期的连续函数，且F′(x)=f(x)，F″(1)=－1，则有

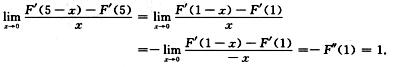
3.奇函数f(x)在闭区间[－1，1]上可导，且|f′(x)|≤M(M为正常数)，则必有(C)

A. |f(x)|≥M．

B. |f(x)|＞M．

C. |f(x)|≤M．

D. |f(x)|＜M．

解析：由于f(x)为奇函数，故f(0)=0．

f(x)在以0，x(－1≤x≤1)为端点的区间上用拉格朗日中值定理，有

|f(x)|=|f(x)－f(0)|=|f′(ξ)||x－0|≤M·1，

故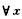

4.设函数f(x)=∫₀^x(t²－4t+3)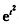(B)

A. f(x)为单调函数．

B. 4e－9为f(x)的一个上界．

C. f(x)的最小值为0．

D. f(x)不存在最大值．

解析：由于f(x)为连续函数，故其在[0，3]上必存在最大值与最小值．选项(D)不正确．

由于

f′(x)=(x²－4x+3)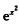=(x－1)(x－3)，

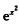故当x∈(0，1)时，f(x)单调增加；当x∈(1，3)时，f(x)单调减少．f(x)在[0，3]上不是单调函数．选项(A)不正确．并且，由f(x)的单调性可知，x=1是f(x)的极大值点，也是最大值点．f(x)的最小值在x=0或x=3处取得．

f(0)=0．

f(3)=∫₀³(t²－4t+3)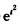=∫₀¹(t²－4t+3)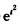+∫₁³(t²－4t+3)本文档预览：3000字符，共14634字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载