
计算机专业(基础综合)模拟试卷292
单选题
1.设n是描述问题规模的非负整数,下面程序片段的时间复杂度是( )。
x=2;
while(x<n/2)
x=2×x;(A)
A. O(log2n)
B. O(n)
C. O(nlog2n)
D. O(n2)
解析:其中,以基本的原操作重复执行的次数作为算法的时间度量。题目中的基本运算是语句x=2×x,设其执行时间为T(n),则有2T(n)<n2 即 T(n) <log2(n2) =0(log2n)。
2.元素a, b,c,d,c依次进入初始为空的栈中,若元素进栈后可停留、可出栈,直到所有元素都出栈,则在所有可能的出栈序列中,以元素d开头的序列个数是( )。(B)
A. 3
B. 4
C. 5
D. 6
解析:d首先出栈后的状态如下图所示。
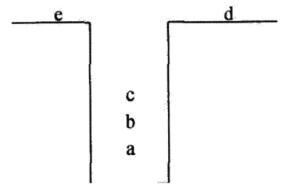
3.已知循环队列存储在一维数组A[0…n-1]中,且队列非空时front和rear分别指向队头元素和队尾元素。若初始时队列为空,且要求第1个进入队列的元素存储在A[0]处,则初始时front和rear的值分别是( )。(B)
A. 0.0
B. 0,n-1
C. n-1,0
D. n-1,n-1
解析:题目要求队列非空时front和rear分别指向队头元素和队尾元素,若初始时队列为空,且要求第1个进入队列的元素存储在A[0]处,则此时front和rear的值都为0。由于进队操作要执行(rear+1)%n,则初始时front的值为0、rear 的值为n-1。
4.若一棵完全二叉树有768个结点,则该二叉树中叶结点的个数是( )。(C)
A. 257
B. 258
C. 384
D. 385
解析:由n=n0+n1+n2和n0=n2+1可知,n=2n0-1+n1,即2n0-1+n1=768,显然n1=1,2n0=768,则n0=384,所以二叉树的叶结点个数是384。还可以根据完全二叉树的另一个性质:最后一个分支结点的序号为[768/2],故非叶子结点数为384,而叶子结点的个数为768-384=384。([x]表示不大于x的最大整数,比如[3.14]=3)。
5.若一棵二叉树的前序遍历序列和后序遍历序列分别为1,2,3,4和4,3,2,1,则该二叉树的中序遍历序列不会是( )。(C)
A. 1,2,3,4
B. 2,3,4,1
C. 3,2,4.1
D. 4,3,2,1
解析:题目中的二叉树的先序序列和后序序列正好相反,这样的二叉树每层只有一个结点。该二叉树的形态如下图所示。
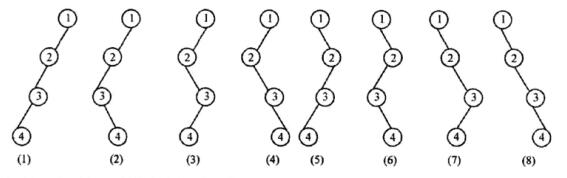
6.已知一棵有2011个结点的树,其叶结点个数为116,该树对应的二叉树中无右孩子的结点个数是( )。(D)
A. 115
B. 116
C. 1895
D. 1896
解析:每个非终端结点转换成二叉树后都对应一个无右孩子的结点(因为一个非终端结点至少有一个孩子结点,其最右边的孩子结点转换成二叉树后一定没有右孩子),另外,树根结点转换成二叉树后也没有右孩子。题目中树的总结点数是2011,叶结点个数是116,则非终端结点个数是2011-116=1895,则该树对应的二叉树中无右孩子的结点个数是1895+1=1896。
7.对于下列关键字序列,不可能构成某二叉排序树中一条查找路径的序列是( )。(A)
A. 95,22,91,24,94,71
B. 92,20,91,34,88,35
C. 21,89,77,29,36,38
D. 12,25,71,68,33,34
解析:各选项对应的查找过程如下图所示,从中看到选项B、C、D对应的查找树都是二叉排序树,只有选项A对应的查找树不是一棵二叉排序树,因为在以91为根的左子树中出现了比91大的结点94。
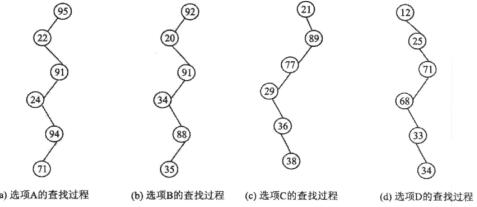
8.下列关于图的叙述中,正确的是( )。
I.回路是简单路径
Ⅱ.存储稀疏图,用邻接矩阵比邻接表更省空间
Ⅲ.若有向图中存在拓扑序列,则该图不存在回路(C)
A. 仅Ⅱ
B. I、Ⅱ
C. 仅Ⅲ
D. I、Ⅲ
解析:第一个顶点和最后一个顶点相同的路径称为回路:序列中顶点不重复出现的路径称为简单路径;回路显然不是简单路径,所以选项I错误。稀疏图用邻接表表示比邻接矩阵节省存储空间,稠密图适合用邻接矩阵的存储表示,所以选项Ⅱ错误。利用拓扑排序算法可以判断图中是否存在回路,即在拓扑排序输出结束后所余下的顶点都有前驱,则说明了只得到了部分顶点的拓扑有序序列,图中存在回路。所以选项Ⅲ正确。
9.为提高散列(Hash)表的查找效率,可以采用的正确措施是( )。
I.增大装填(载)因子
Ⅱ.设计冲突(碰撞)少的散列函数
Ⅲ.处理冲突(碰撞)时避免产生聚集(堆积)现象(D)
A. 仅I
B. 仅Ⅱ<
本文档预览:3000字符,共23749字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载