考研数学一（中值定理与一元函数微分学的应用）模拟试卷16

考研数学一（中值定理与一元函数微分学的应用）模拟试卷16

选择题

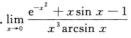1.(B)

A. 1／2

B. 1／3

C. 2／3

D. 3／4

解析：由麦克劳林公式得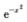=1-x²+x⁴／2+ο(x⁴)，sin x=x-x³／6+ο(x³)，则

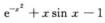=1／3x⁴+ο(x⁴)～1／3x⁴，

故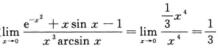

2.设f(x)二阶可导，f’’(2)=0，且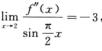(C)

A. x=2为f(x)的极大值点

B. x=2为f(x)的极小值点

C. (2，f(2))为曲线y=f(x)的拐点

D. (2，f(2))不是曲线y=f(x)的拐点，x=2也不是f(x)的极值点

解析：因为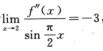

3.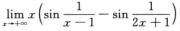(D)

A. -1

B. 1

C. -1／2

D. 1／2

解析：令f(t)=sin t，f’(t)=cos t，则

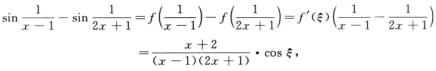
其中ξ介于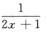与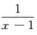之间，则原式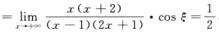

4.设f(x)连续，且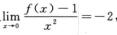(D)

A. f(x)在x=0处不可导

B. f(x)在x=0处可导且f’(0)≠0

C. f(x)在x=0处取极小值

D. f(x)在x=0处取极大值

解析：由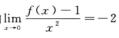得f(0)=1．

由极限的保号性可知，存在δ＞0，当0＜｜x｜＜δ时，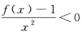

5.设f(x)二阶连续可导，f’(0)=0，且(A)

A. x=0为f(x)的极大值点

B. x=0为f(x)的极小值点

C. (0，f(0))为曲线y=f(x)的拐点

D. x=0不是f(x)的极值点，(0，f(0))也不是曲线y=f(x)的拐点

解析：因为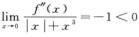，所以由极限的保号性可知，存在δ＞0，当0＜｜x｜＜δ时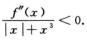，．注意到x³=ο(x)，所以当0＜｜x｜＜δ时，f’’(x)＜0．

从而f’(x)在(-δ，δ)内单调递减，再由f’(0)=0得

6.设f(x)在(-∞，+∞)内二阶可导，f’’(x)＜0，且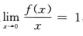(B)

A. 单调递增且大于零

B. 单调递增且小于零

C. 单调递减且大于零

D. 单调递减且小于零

解析：由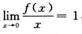

7.设f(x)=x³+ax²+bx在x=1处有极小值-2，则( )．(C)

A. a=1，b=2

B. a=-1，b=-2

C. a=0．b=-3

D. a=

本文档预览：3000字符，共9474字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载