
考研数学一(定积分及应用)模拟试卷3
选择题
1.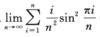 (D)
(D)
A. 1/2
B. π/2
C. π/4
D. 1/4
解析:
 1/π2∫0πtsin2tdt=1/π2·π/2∫0πsin2tdt
1/π2∫0πtsin2tdt=1/π2·π/2∫0πsin2tdt

2.下列反常积分收敛的是( ).(D)
A. 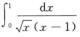 B.
B. 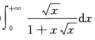 C.
C. 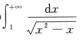 D.
D. 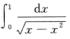 解析:由
解析:由 且α=1≥1得
且α=1≥1得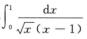 发散,排除A项;
发散,排除A项;
由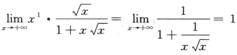 且α=1≤1得
且α=1≤1得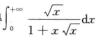 发散,排除B项;
发散,排除B项;
由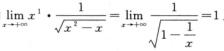 且α=1≤1得
且α=1≤1得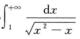 发散,排除C项,
发散,排除C项,
选D.事实上,因为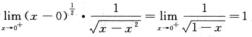 且α=1/2<1,又因为
且α=1/2<1,又因为
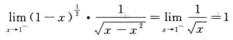 且α=1/2<1,故
且α=1/2<1,故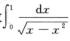
3.设f(x)连续,且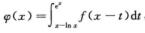 (C)
(C)
A. f(ln x)=f(x-ex)
B. f(x-ex)-f(ln x)
C. 1/xf(ln x)-(1-ex)f(x-ex)
D. (1-ex)f(x-ex)-1/xf(ln x)
解析: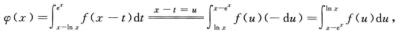
4.下列反常积分收敛的是( ).(D)
A. ∫-121/x2dx
B. 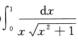 C.
C. 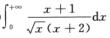 D.
D. 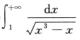 解析:方法一 ∫-121/x2dx=∫-101/x2dx+∫021/x2dx.
解析:方法一 ∫-121/x2dx=∫-101/x2dx+∫021/x2dx.
因为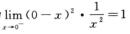 且α=2>1,所以∫-101/x2dx发散,故∫-121/x2dx发散;
且α=2>1,所以∫-101/x2dx发散,故∫-121/x2dx发散;
因为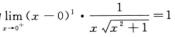 且α=
且α=
本文档预览:3000字符,共13331字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载
