
考研数学一(中值定理与一元函数微分学的应用)模拟试卷14
选择题
1.设f(x)=arcsin x,对x≠0,f(x)-f(0)=xf’(θx)(0<θ<1),则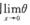 (C)
(C)
A. 1/2
B.  C.
C. 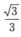 D. 1/3
D. 1/3
解析:由f(x)-f(0)=xf’(θx)得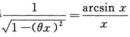 ,解得
,解得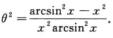

则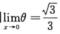
2.设f(x)为连续函数,且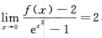 (A)
(A)
A. x=0为f(x)的极小值点
B. x=0为f(x)的极大值点
C. x=0不是f(x)的极值点
D. (0,2)为y=f(x)的拐点
解析:因为f(x)连续,所以由 得f(0)=2,且存在δ>0,当0<|x|<δ时,
得f(0)=2,且存在δ>0,当0<|x|<δ时,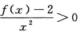
3.设函数y=y(x)由y3-y2+y+x2-2x=0确定,则( ).(A)
A. y=y(x)的极大值点为x=1,极大值为y=1
B. y=y(x)的极小值点为x=1,极小值为y=1
C. y=y(x)的极大值点为x=-1,极大值为y=1
D. y=y(x)的极小值点为x=-1,极小值为y=1
解析:y3-y2+y+x2-2x=0两边对x求导得
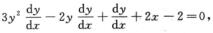
令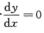 得x=1,代入原方程得y3-y2+y=1,解得y=1.
得x=1,代入原方程得y3-y2+y=1,解得y=1.
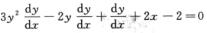 再对x求导得
再对x求导得
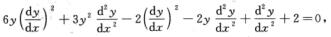
4.设f(x)=aresin x,对a≠0有f(a)=f’(aθ)a,则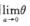 (D)
(D)
A. 1/2
B.  C. 1/3
C. 1/3
D. 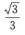 解析:
解析: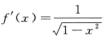 ,由
,由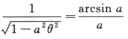 得
得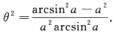
由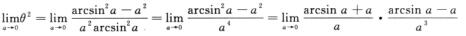
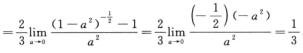 ,故
,故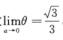
5.设f’(0)=0,且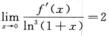 (B)
(B)
A. f(0)不是f(x)的极值
B. f(0)是f(x)的极小值
C. f(0)是f(x)的极大值
D. (0,f(0))是曲线y=f(x)的拐点
解析:因为
