考研数学一（不定积分）模拟试卷20

考研数学一（不定积分）模拟试卷20

填空题

1.

1／4(2x+1)-1／4ln｜2x+1｜+C．

解析：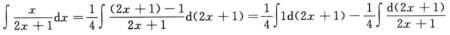

2.

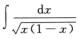
[*]或arcsin(2x-1)+C．

解析：方法一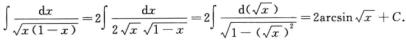

方法二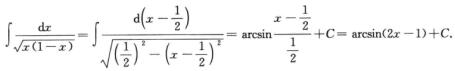

3.

[*]

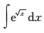
解析：令，x=t²，dx=2tdt，则

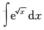=2∫te^tdt=2∫td(e^t)=2te^t-2∫e^tdt=2te^t-2e^t+C=

4.

1／2arctansin²x／2+C．

解析：因为(sin²x)’=sin 2x，所以

5.

[*]

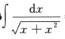
解析：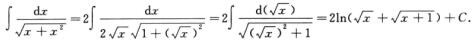

6.

[*]

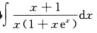
解析：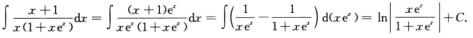

7.

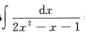
1／3ln｜x-1｜-1／3ln｜2x+1｜+C．

解析：令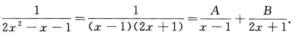

由A(2x+1)+B(x-1)=1得A=1／3，B=-2／3，则

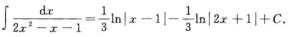
8.∫xtan²xdx=________．

xtan x+ln｜cos x｜-x²／2+C．

解析：∫xtan²xdx=∫x(sec²x-1)dx=∫xd(tan x)-x²／2

=xtan x-∫tan x dx-x²／2=xtan x+ln｜cos x｜-x²／2+C．

解答题

计算下列不积分

9.

[*]

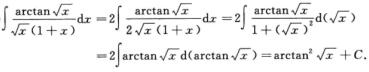
解析：

10.

[*]

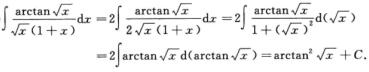
解析：

11.

[*]

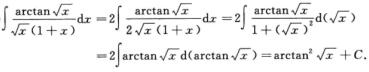
解析：

12.

[*]

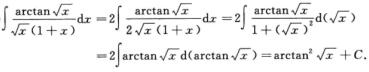
解析：

计算下列不积分

13.∫arcsin xarccos xdx．

∫arcsin xarccos xdx=[*]

=xa

本文档预览：3000字符，共5025字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载