考研数学一（向量代数与空间解析几何）模拟试卷17
选择题
1.点M(1，-1，2)关于平面π：x-2y+z+1=0对称的点为( )．(D)
A. (1，3，0)
B. (1，-3，0)
C. (-1，3，1)
D. (-1，3，0)
解析：过点M与平面π垂直的直线L：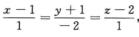
，转化为参数方程得L：
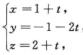，代入平面π的方程得t=-1，则直线L与平面π的交点坐标为T(0，1，1)，\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t
设对称点为N(a，b，c)，由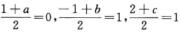
2.过点M(1，-1，1)及直线L：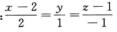
(B)
A. x+y+z-3=0
B. x-y+z-3=0
C. x-y+2z-3=0
D. 2x-y+z-3=0
解析：点M0(2，0，1)∈L，s={2，1，-1}，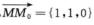
3.平面π1：2x-y+z-1=0与平面π2：-x+2y+z+4=0的夹角为( )．(C)
A. π
B. π／2
C. π／3
D. π／6
解析：两个平面的法向量为n1={2，-1，1}，n2={-1，2，1}，设两平面的夹角为θ，cos θ=
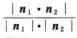
4.设直线L1：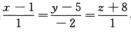
，L2：
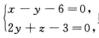(C)
A. π／6
B. π／4
C. π／3
D. π／2
解析：s1={1，-2，1}，s2={1，-1，0}×{0，2，1}={-1，-1，2}．
设直线L1，L2的夹角为θ，则
填空题
5.设a，b为单位向量，且两向量的夹角为π／4，则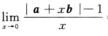
[*]
解析：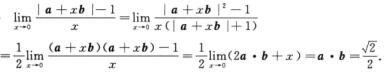
6.曲线L：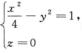
x2／4-y2+z2／4=1．
解析：所求的曲面为∑：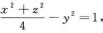
7.过点M(1，-1，2)且与平面π1：x-y+z-2=0，π2：2x+y-z+1=0都垂直的平面为________．
y+z-1=0．
解析：所求平面的法向量为
n={1，-1，1}×{2，1，-1}={0，3，3}，\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t
所求的平面方程为π：0(x-1)+3(y+1)+3(z-2)=0，即\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t
π：y+z-1=0．
8.若
[*]
解析：由｜a+b｜2=(a+b)(a+b)=｜a｜2+｜b｜2+2ab=13+19+2ab=24，得ab=-4，则｜a-b｜2=(a-b)(a-b)=｜a｜2+｜b｜2-2ab=13+19+8=40．
则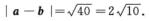
9.过原点及点(6，-3，2)且与平面4x-y+2z=8垂直的平面方程为________．
2x+2y-3z=0．
解析：设所求平面为π：Ax+By+Cz+D=0，因为π经过原点，
本文档预览：3000字符，共7635字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
