考研数学一（导数与微分）模拟试卷15

考研数学一（导数与微分）模拟试卷15

选择题

1.设f(x)以2为周期且f’(1)=π，则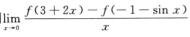(C)

A. π

B. 2π

C. 3π

D. 4π

解析：由f(3+2x)=f(2+1+2x)=f(1+2x)，f(-1-sin x)=f(-2+1-sin x)=f(1-sin x)得

2.设函数y=f(x)连续，△y=2x△x+ο(△x)，且f(1)=2，则函数y=f(x³)在x=1处的微分为( )．(C)

A. 2dx

B. 3dx

C. 6dx

D. 9dx

解析：由△y=2x△x+ο(△x)得f(x)可导，且f’(x)=2x，则f(x)=x²+C．

由f(1)=2得C=1，从而f(x)=x²+1，于是y=f(x³)=x⁶+1，f’(x³)=6x⁵，则y=f(x³)在x=1处的微分为6dx，选C．

3.设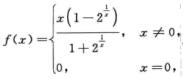(C)

A. f(x)在x=0处连续可导

B. f(x)在x=0处可导，但导数不连续

C. f(x)在x=0处不可导但连续

D. f(x)在x=0处不连续

解析：由f(0-0)=f(0)=f(0+0)=0得f(x)在x=0处连续；又因为

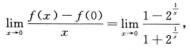
而由得f’_–(0)=1；再由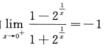

4.设函数f(x)在｜x｜＜δ内有定义且｜f(x)｜≤x²，则f(x)在x=0处( )．(C)

A. 不连续

B. 连续但不可微

C. 可微且f’(0)=0

D. 可微但f’(0)≠0

解析：显然f(0)=0，且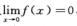，所以f(x)在x=0处连续．

又由｜f(x)｜≤x²得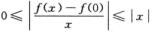，根据夹逼定理得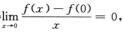

5.下列结论正确的是( )．(D)

A. 若f(x)，g(x)在x=a处不可导，则f(x)g(x)在x=a处一定不可导

B. 若f(x)，g(x)在x=a处不可导，则f[g(x)]在x=a处一定不可导

C. 若f(x)，g(x)在x=a处不可导，则f(x)+g(x)在x=a处一定不可导

D. 若f(x)在x=a处可导且f(a)≠0，则｜f(x)｜在x=a处一定可导

解析：取f(x)=x^1／3，g(x)=x^2／3，显然f(x)，g(x)在x=0处不可导，但f(x)g(x)=x在x=0处可导；

取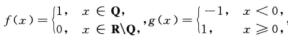，显然f(x)，g(x)在x=0处不可导，但f[g(x)]≡1在x=0处可导；

取f(x)=x+｜x｜，g(x)=x-｜x｜，显然f(x)，g(x)在x=0处不可导，但f(x)+g(x)=2x在x=0处可导．

事实上，设f(a)＞0，因为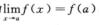，所以存在δ＞0，当x∈(a-δ，a+δ)时，f(x)＞0，则

6.设φ(x)连续，f(x)=｜x-a｜φ(x)，则f(x)在x=a处可导的充要条件是( )．(C)

A. φ(a)=1

B. φ(a)=-1

C. φ(a)=0

D. φ’(a)=0

解析：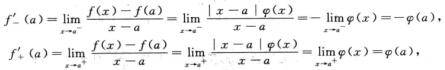

7.若f(-x)=-f(x)，且在(0，+∞)内f’(x)＞0，f’’(x)＞0，则在(-∞，0)内( )．(C)

A. f’(x)＜0，f’’(x)＜0

B. f’(x)＜0，f’’(x)＞0

C. f’(x)＞0，f’’(x)＜0

D. f’(x)＞0，f’’(x)＞0

解析：因为f(x)为奇函数，所以f’(x)为偶函数，f’’(x)为奇函数，故在(-∞，0)内有f’(x)＞0，在(-∞，0)内有f’’(x)＜0，选C．本文档预览：3000字符，共8018字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载