
考研数学一(函数、极限、连续)模拟试卷58
选择题
1.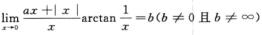 (B)
(B)
A. a=0,b=-π/2
B. a=0,b=π/2
C. a=1,b=π/2
D. a=-1,b=π/2
解析:
因为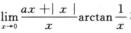
2.设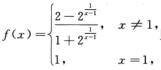 (C)
(C)
A. f(x)在x=1处连续
B. x=1为f(x)的可去间断点
C. x=1为f(x)的跳跃间断点
D. x=1为f(x)的第二类间断点
解析:由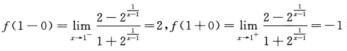
3.当x→0时,下列无穷小中,哪个是比其他三个更高阶的无穷小( ).(D)
A. x2
B. 1-cos x
C.  D. x-tan x
D. x-tan x
解析:当x→0时,1-cos x~x2/2,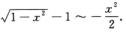
因为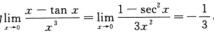
4.设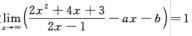 (B)
(B)
A. a=-1,b=3/2
B. a=1,b=3/2
C. a=1,b=-3/2
D. a=-1,b=-3/2
解析:由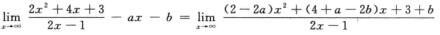 得
得
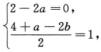
5.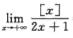 (B)
(B)
A. 0
B. 1/2
C. 1
D. ∞
解析:对任意的x>0,存在n∈N,使得x=n+θ,其中0≤θ<1,且当x→+∞时,n→∞,由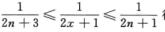 得
得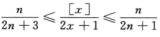 ,再由夹逼定理得
,再由夹逼定理得
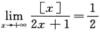
6.设 (B)
(B)
A. 连续点
B. 第一类间断点
C. 第二类间断点
D. 不能判断连续性的点
解析:当x>0时,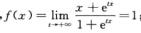
填空题
7.设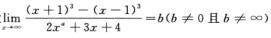
2,3.
解析:由(x+1)3=x3+3x2+3x+1,(x-1)3=x3-3x2+3x-1得(x+1)3-(x-1)3=6x2+2,则a=2,b=3.
8.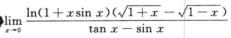
2.
解析:当x→0时,ln(1+xsinx)~xsinx~x2,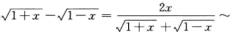
x,tan x-sin x=tan x(1-cos x)~x·1/2x2-x3/2,则
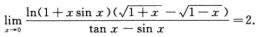
9.设a>0,且
