考研数学一（微分方程）模拟试卷12

考研数学一（微分方程）模拟试卷12

选择题

1.设φ₁(or)，φ₂(x)为y’+a(x)y=b(x)的两个不同的解，则y’+a(x)y=b(x)的通解为( )．(C)

A. y=Cφ₁(x)

B. y=Cφ₁(x)+φ₂(x)

C. y=C[φ₂(x)-φ₁(x)]+φ₂(x)

D. y=C₁φ₁(x)+C₂φ₂(x)

解析：因为φ₂(x)-φ₁(x)为y’+a(x)y=0的一个非零解，所以y’+a(x)y=0的通解为y=C[φ₂(x)-φ₁(x)]．

又因为φ₂(x)为y’+a(x)y=b(x)的一个特解，所以y’+a(x)y=b(x)的通解为y=C[φ₂(x)-φ₁(x)]+φ₂(x)，选C．

2.设y₁=2x-e^x，y₁=2x+e^x为y’+a(x)y=b(x)的两个特解，则( )．(C)

A. a(x)=1，b(x)=2x

B. a(x)=-1，b(x)=2x

C. a(x)=-1，b(x)=2-2x

D. a(x)=-1，b(x)=2+2x

解析：令 y’+a(x)y=0， (1)

显然y₀=y₂-y₁=2e^x为(1)的特解，代入得a(x)=-1．\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t

显然y₃=1／2y₁+1／2y₂=2x为y’-y=b(x)的特解，代入得b(x)=2-2x，选C．\\t

3.设y₁(x)，y₂(x)为一阶非齐次线性微分方程y’+p(x)y=q(x)的两个特解，且ky₁(x)+ly₂(x)为y’+p(x)y=0的特解，ky₁(x)-2ly₂(x)为y’+p(x)y=q(x)的特解，则( )．(B)

A. k=1／3，l=1／3

B. k=1／3，l=-1／3

C. k=-1／3，l=-1／3

D. k=-1／3，l=1／3

解析：由线性微分方程解的结构得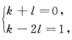

4.微分方程y’’-4y=e^2x+x的特解形式为( )．(D)

A. ae^2x+bx+x

B. ax²e^2x+bx+c

C. axe^2x+bx²+cx

D. axe^2x+bx+c

解析：y’’-4y=0的特征方程为λ²-4=0，特征根为λ₁=-2，λ₂=2．

y’’-4y=e^2x的特解形式为y₁=axe^2x，y’’-4y=x的特解形式为y₂=bx+c，故原方程的特解形式为axe^2x+bx+c，选D．

5.设y₀=e^2x+(x+2)e^x为y’’+ay’+by=ce^x的特解，则( )．(C)

A. a=-2，b=1，c=-1

B. a=3，b=2，c=-1

C. a=-3，b=2，c=-1

D. a=-3，b=2，c=1

解析：显然e^2x为y’’+ay’+by=0的一个特解，则λ₁=2；

由特解形式得y’’+ay’+by=0的另一个特征值为λ₂=1，则a=-3，b=2．\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t

因为λ₂=1为单的特征值，所以xe^x为y’’+ay’+by=ce^x的特解，代入得c=-1，选C．

填空题

6.(1+y²)dx-2xydy=0(x＞0)满足y(1)=0的特解为________．

x=1+y²．

解析：由(1+y²)dx-2xydy=0得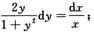

7.以y₀=2e^xcos 2x为特解的二阶常系数齐次线性微分方程为________．

y’’-2y’+5y=0．

解析：y₀=2e^xcos 2x为二阶常系数齐次线性微分方程的特解，其特征值为λ₁=1+2i．

λ₂=1-2i，其特征方程为\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t

(λ-1-2i)(λ-1+2i)=0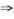

8.微分方程xy’+

本文档预览：3000字符，共10262字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载