
考研数学一(定积分及应用)模拟试卷2
选择题
1.设φ(x)=∫0xt2f(x3-t3)dt,其中f(u)可导,则φ’(x)=( ).(B)
A. f(x3)
B. x2f(x3)
C. f’(x3)
D. x2f’(x3)
解析:φ(x)=∫0xt2f(x3-t3)dt=-1/3∫0xf(x3-t3)d(x3-t3)
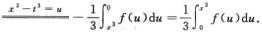
2.下列反常积分收敛的是( ).(C)
A. 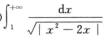 B.
B. 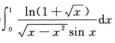 C.
C. 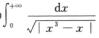 D.
D. 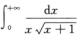 解析:方法一 因为
解析:方法一 因为 且α=1≤1,所以
且α=1≤1,所以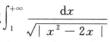 发散;
发散;
因为 且α=1≥1,所以广义积分
且α=1≥1,所以广义积分
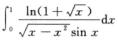 发散;
发散;
因为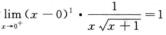 且α=1≥1,所以
且α=1≥1,所以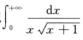 发散,选C.
发散,选C.
方法二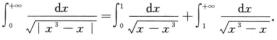
因为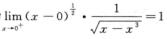 且α=1/2<1,又因为
且α=1/2<1,又因为
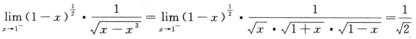 且α=1/2<1,
且α=1/2<1,
所以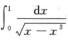 收敛;
收敛;
因为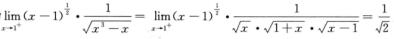 且α=1/2<1,
且α=1/2<1,
又因为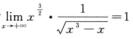 且α=3/2>1,所以
且α=3/2>1,所以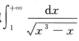 收敛,故
收敛,故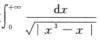
3.设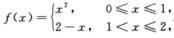 (B)
(B)
A. 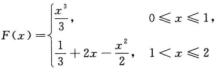 B.
B. 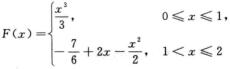 C.
C. 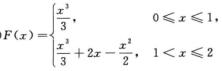 D.
D. 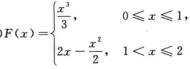 解析:当0≤x≤1时,F(x)=∫0xt2dt=x3/3;当1<x≤2时,F(x)=∫0xf(t)dt=∫01t2dt+∫1x(2-t)dt=1/3+2x-2-x2/2+1/2=-7/6+2x-x2/2.
解析:当0≤x≤1时,F(x)=∫0xt2dt=x3/3;当1<x≤2时,F(x)=∫0xf(t)dt=∫01t2dt+∫1x(2-t)dt=1/3+2x-2-x2/2+1/2=-7/6+2x-x2/2.
选B.
4.下列广义积分发散的是( ).(A)
A. ∫-111/sinxdx
B. 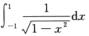 C.
C. 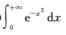 D.
D. 
