考研数学一（三重积分与曲线、曲面积分）模拟试卷7

考研数学一（三重积分与曲线、曲面积分）模拟试卷7

选择题

1.设f(x)连续，且f(0)=0，f’(0)=1，若Ω={(x，y，z)｜x²+y²+z²≤t²，z≥0}(t＞0)，则(B)

A. π／4

B. π／2

C. 3π／4

D. π

解析：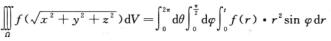

=2π∫₀^π／2sin φdφ∫₀^tf(r)·r²dr=2π∫₀^tf(r)·r²dr\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t

则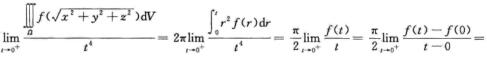

2.设L：从点A(-1，0)到点B(1，0)，则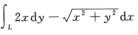(C)

A. π+2

B. π-2

C. -π-2

D. -π+2

解析：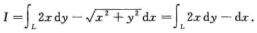

L的参数方程为L：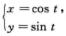

3.设Ω={(x，y，z)｜x²+y²+z²≤2z}，则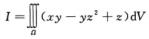(D)

A. π／3

B. 2π／3

C. π

D. 4π／3

解析：由对称性得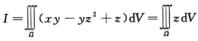，令

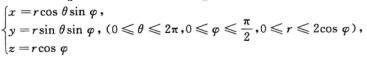\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t

则I=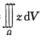

4.设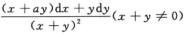(D)

A. -1

B. 0

C. 1

D. 2

解析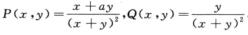：Q(x，y)=y／(x+y)²，由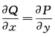

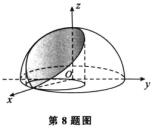
5.设上半球面x²+y²+z²=4(z≥0)被柱面x²+y²=2x所截曲面为∑，则

(D)

A. π

B. 3π／2

C. 2π

D. 5π／2

解析：如图所示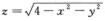，∑：，D：x²+y²≤2x，则

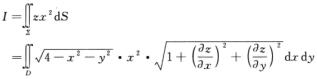\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t

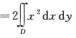=2∫_-π／2^π／2cos²θdθ∫₀^{2cos θ}r³dr=8∫_-π／2^π／2cos⁶θdθ

=16∫₀^π／2cos⁶θdθ=16·5／6·3／4·1／2·π／2=5π／2，选D．\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t\\t

填空题

<

本文档预览：3000字符，共15301字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载