考研数学三（微积分）模拟试卷277

考研数学三（微积分）模拟试卷277

选择题

1.∫₀^+∞dy∫_y^2y(D)

A. 1

B. 1／2

C. 1／3

D. 1／4

解析：积分区域如图所示．

∫₀^+∞dy∫_y^2ydx=∫₀^+∞dx

=-1／4∫₀^+∞d(-x²)=-

2.若二阶常系数齐次微分方程y’’+ay’+by=0的解在(-∞，+∞)上均有周期性，则( )．(D)

A. a＜0，b＜0

B. a＞0，b＞0

C. a=0，b＜0

D. a=0，b＞0

解析：微分方程y’’+ay’+by=0的特征方程为r²+ar+b=0，其判别式△=a²-4b．

当△＞0时，特征方程有两个不同的解，设为r₁，r₂，则

y=C₁

3.设下列A，B，C为任意常数，则微分方程y’’+4y=sin²x有特解形如( )．(D)

A. Asin²x

B. Acos²x

C. x(A+Bcos2x+Csin2x)

D. A+x(Bcos2x+Csin2x)

解析：原方程可以y’’+4y=1／2-cos2x／2．对应齐次方程的特征方程为r²+4=0，得r_1，2=±2i，故由待定系数法可知该方程有形如(D)的特解．

4.微分方程y’+xy=(C)

A. 1

B. 2

C. 3

D. 4

解析：由题意得

由y(0)=0，得C=0，所以

y(x)=x

y’(x)=(1-x²)

y’’(x)=(-3x+x³)

令y’’(x)=0，得

x₁=0，x₂=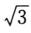，x₃=-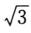

5.设a_n=cosnπln，n=1，2，…，则( )．

(C)

A.

B.

C.

D.

解析：由题意知，a_n=(-1)ⁿln(1+)，令u_n=ln(1+)，由于u_n=0，{u_n}单调不增，根据莱布尼茨判别法知a_n收敛，又a_n²=ln²(1+)，在n→∞时，In²(1+本文档预览：3000字符，共15729字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载