考研数学三（微积分）模拟试卷280

考研数学三（微积分）模拟试卷280

选择题

1.∫_-1¹dy|x|y²dx=( )．

(B)

A.

B.

C.

D.

解析：由题意可知，积分区域D={(x，y)|-1≤y≤1，-π／2≤x≤arctany}，如图所示交换积分次序，则

2.已知函数y=y(x)在任意点x处的增量△y=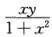(A)

A. B. C. 2

D. 2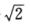解析：由题设得，分离变量得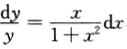，两边积分得

ln||y|=1／2ln(1+x²)+lnC₁，

即y=±C₁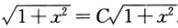。由于y(0)=1，故C=1，即y=

故y’(1)=

3.若某三阶常系数齐次线性微分方程具有特解y=2xe^x与y=3e^-2x，则该微分方程为( )．(D)

A. y’’’-y’’-4y’+4y=0

B. y’’’+3y”-4y=0

C. y’’’+2y’’-y’-2y=0

D. y’’’-3y’+2y=0

解析：由题设知，微分方程的特征方程为(r-1)²(r+2)=0，即r³-3r+2=0．故所求微分方程为y’’’-3y’+2y=0．

应选(D)．

填空题

4.∫₀¹dx∫₁^x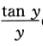

lncos1

解析：∫₀¹dx∫₁^x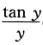dy=-∫₀¹dy∫₀^ydx

=-∫₀¹ydy

=-∫₀¹

5.∫_-1¹dx

22／15

解析：积分区域如图所示，则

∫_-1¹dx(x+1)ydy

∫_-1¹dxydy

=2∫₀¹dxydy

=∫₀¹(y²)dx

=∫₀¹(2-x²-x⁴)dx

=(2x-x³／3-x⁵

本文档预览：3000字符，共15059字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载