考研数学三（微积分）模拟试卷264

考研数学三（微积分）模拟试卷264

选择题

1.设f(x)是(-∞，+∞)上可导的奇函数，任意的x∈(-∞，+∞)，均有f(x+1)-f(x)=f(1)，f(1／2)=0，则以下是偶函数的是( )．(A)

A. ∫₀^x[sinf(t)+f(t+1)]dt

B. ∫₀^x[sinf’(t)+f’(t+1)]dt

C. ∫₀^x[cosf(t)+f(t+2)]dt

D. ∫₀^x[cosf’(t)+f’(t+2)]dt

解析：令x=-1／2，代入题设等式，有

2.当x→0时，α(x)与β(x)是非零且不相等的等价无穷小量，以下4个结论：

①α(x)+β(x)=2α(x)；

②α(x)+β(x)=2β(x)；

③α(x)-β(x)=o(α(x))；

④α(x)-β(x)=o(β(x))；

所有正确结论的序号是( )．(B)

A. ①③

B. ③④

C. ①②③④

D. ②④

解析：由α(x)与β(x)是非零且不相等的等价无穷小量，得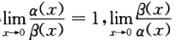=1，α(x)≠0，β(x)≠0且α(x)≠β(x)，从而

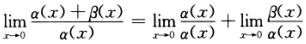=1+1=2

故α(x)+β(x)～2β(x)，不是“=”，①错误；

同理，α(x)+β(x)～2β(x)，从而②错误；

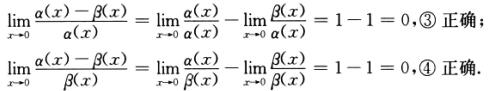
3.已知数列{x_n}，其中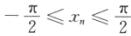(A)

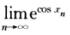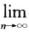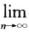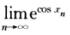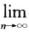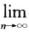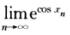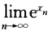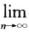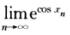A. 当存在时，cosx_n存在，且B. 当存在时，cosx_n存在，且C. 当存在时，cosx_n存在，且D. 当存在时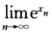，cosx_n存在，且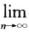解析：对于选项(B)，(C)，(D)，令x_n=(-1)ⁿ，则=e^cos1存在，此时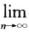cosx_n=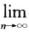(-1)ⁿ=cos1存在，但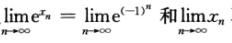

4.设函数f(x)在x=0处三阶可导，则下列命题中

(C)

A. ①②

B. ①③

C. ②④

D. ③④

解析：由题设知f’’(0)存在，则f(x)，f’(x)在x=0处都连续．

由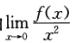及洛必达法则，可得

本文档预览：3000字符，共11619字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载