考研数学三（微积分）模拟试卷275

考研数学三（微积分）模拟试卷275

选择题

1.设函数f(x)=x(2x-3)(4x-5)，则方程f’(x)=0的实根个数为( )．(C)

A. 0

B. 1

C. 2

D. 3

解析：f(x)=0的实根为x₁=0，x₂=5／4，x₃=3／2，即f(，0)=f(5／4)=f(3／2)，且f(x)可导，则由罗尔定理，存在a∈(0，5／4)，使f’(ξ₁)=0；存在ξ₂∈(5／4，3／2)，使f’(ξ₂)=0．故f’(x)=0至少有两个实根．又f’(x)=0为一元二次方程，至多有两个实根．综上，选(c)．

2.设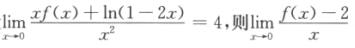(C)

A. 2

B. 4

C. 6

D. 8

解析：

3.设函数f(x)具有连续导数，且(A)

A. 当f(0)=0时，f(x)是f(x)的极大值

B. 当f(0)=0时，f(0)是f(x)的极小值

C. 当f(0)＞0时，f(0)是f(x)的极大值

D. 当f(0)＜0时，f(0)是f(x)的极小值

解析：因为函数f(x)具有连续导数，且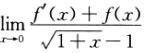=-1，所以

f’(0)+f(0)=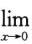[f’(x)+f(x)]=0．

若f(0)≠0，则f’(0)≠0，故f(0)不是f(x)的极值．

若f(0)=0，则f’(0)=0，从而

4.设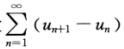收敛，则下列级数中收敛的是( )．

(D)

A.

B.

C.

D.

解析：方法一因为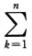(u_k+1-u_k)=u_n+1-u₁，(u_n+1-u_n)收敛，即有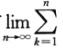(u_k+1-u_k)=(u_n+1-u₁)存在，所以可以得到{u_n}收敛，从而{u_n²}收敛．

因为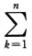(u_k+1²-u_k²)=u_n+1²-u₁²，所以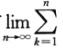(u_k+1²-u_k²)=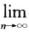(u_n+1²-u₁²)存在，即(u_n+1²-u_n²)收敛

方法二取u_n=1-1／n，则(u_n+1-u_n)收敛，这时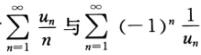均发散，故可排除A，B．

取u_n=-1／n，则(u_n+1-u_n)收敛，且1-

5.已知F(a，b)=本文档预览：3000字符，共12759字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载