考研数学三（微积分）模拟试卷258

考研数学三（微积分）模拟试卷258

选择题

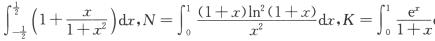1.设M=(C)

A. M＞N＞K

B. N＞K＞M

C. K＞M＞N

D. K＞N＞M

解析：M=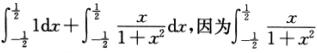dx=0，所以M=1．

令g(x)=(1+x)ln²(1+x)-x²(0≤x≤1)，则有

g’(x)=ln²(1+x)+(1+x)2ln(1+x)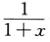-2x=ln²(1+x)+2ln(1+x)-2x，

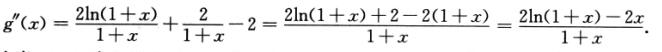
因为当x＞0时，ln(1+x)＜x，所以ln(1+x)-x＜0，即有g’’(x)＜0，g’(x)在区间[0，1]上单调减少，所以g’(x)＜g’(0)=0(0＜x≤1)，即g(x)在区间[0，1]上单调减少，所以g(x)＜g(0)=0(0＜x≤1)，即(1+x)ln²(1+x)-x²＜0(0＜x≤1)，故

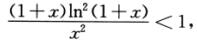
所以∫₀¹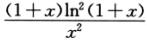dx＜∫₀¹1dx=1，即N＜M．

当x＞0时，e^x＞1+x，所以

2.若函数f(x)连续，g(x)=∫₀^2xf(x+t／2)dt，则当x_j0⁺+时，g(x)是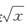(A)

A. 高阶无穷小

B. 低阶无穷小

C. 等价无穷小

D. 同阶非等价无穷小

解析：在g(x)=∫₀^2x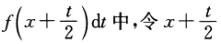=u，则

g(x)=∫₀^2xf(x+t／2)dt=2∫_x^2xf(u)du，

这表明当x→0⁺时，g(x)是

3.设f(x，y)在有界闭区域D上连续，在D内有一阶偏导数．若f(x，y)在D的边界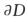上的值均为0，且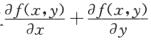(D)

A. 在D内有正的最大值

B. 在D内有负的最小值

C. 只在D的边界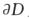D. 在D的边界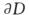解析：设在D内存在(x₀，y₀)，使得f(x₀，y₀)为正的最大值，则f(x₀，y₀)＞0，且

f’_x(x₀，y₀)=0，f’_y(x₀，y₀)=0．

由题设条件得f’_x(x₀，y₀)+f’_y(x₀，y₀)=f(x₀，y₀)=0，矛盾，故选项(A)不正确．

同理，选项(B)也不正确．

故对于任意(x，y)∈D，f(x，y)=0，故f(x，y)在D的边界上和D的内部处处为最大值，处处为最小值．

4.设f(x)在x=a处可导，则|f(x)|在x=a处不可导的充分必要条件是( )．(B)

A. f(a)=0，f’(a)=0

B. f(a)=0，f’(a)≠0

C. f(a)≠0，f’(a)=0

D. f(a)≠0，f’(a)≠0

解析：若f(a)≠0，则存在x=a的某邻域U(a)，在该邻域内f(x)与f(a)同号．于是推知，若f(a)＞0，则|f(x)|=f(x)(当x∈U(a))；若f(a)＜0，则|f(x)|=-f(x)．总之，若f(a)≠0，|f(x)|在x=a处总可导．

若f(a)=0，则

本文档预览：3000字符，共11117字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载