考研数学三（微积分）模拟试卷274

考研数学三（微积分）模拟试卷274

选择题

1.曲线y=xln(e+1／x)的斜渐近线为( )．(C)

A. y=x+e

B. y=x-e

C. y=x+1／e

D. y=x-1／e

解析：由于

2.设函数f(x，y)在点(0，1)的某邻域内一阶偏导数连续，f(0，1)=0，f’_y(0，1)=1，则f(x，∫₁^tlnxdx)=0( )．(C)

A. 在点(0，1)附近可确定t=t(x)，且t’(0)=-f’_x(0，1)

B. 在点(0，1)附近可确定t=t(x)，且t’(0)=-1

C. 在点(0，e)附近可确定t=t(x)，且t’(0)=-f’_x(0，1)

D. 在点(0，e)附近可确定t=t(x)，且t’(0)=-1

解析：记F(x，t)=f(x，∫₁^tlnxdx)

F’_x=f’₁，

F’_t=f’₂lnt，

在(0，e)处，有F’_x|_0，e=f’₁(0，1)

F’_t|_0，e=f’₂(0，1)=1

故在(0，e)附近可确定t=t(x)，且

t’(0)=-

3.设u_n=，k为正常数，则(B)

A. 绝对收敛

B. 条件收敛

C. 发散

D. 敛散性与k有关

解析：令f(x)=arctan(x+k)-arctanx，

得f’(x)=＜0

则f(x)单调减少，即u_n单调减少．

则u_n发散，又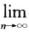u_n=0，

由莱布尼茨判别法可知，

4.设f(x)连续，当x→0时，e^f(x)-1与x-ln(1+x)是等价无穷小量，以下结论：

①f(x)在x=0处取得极大值；

②(0，f(0))是曲线f(x)的拐点；

③f(x)在x=0处的2次泰勒多项式为x²／2．

正确结论的个数为( )．(B)

A. 0

B. 1

C. 2

D. 3

解析：由题意，f(x)=0=f(0)．

又当x→0时，x-ln(1+x)～x²／2，故

即f’(0)=0．又=1+α，其中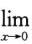

5.设f(x)=x²，f[φ(x)]=-x²+2x+3且φ(x)≥0，则(A)

A. 1／12

B. 1／6

C. 1／3

D. 2／3

解析：由题设，f[φ(x)]=φ²(x)=-x²+2x+3，且φ(x)≥0，则

φ(x)=

其中-x²+2x+3≥0，即(x-3)(x+1)≤0，解得-1≤x≤3，即[-1，3]为φ(x)的定义域．

又(-x²+2x+3)’=-2x+20，解得x=1，故当-1≤x＜1时，导数大于0；当1＜x≤3时，导数小于0．所以φ(1)=2为最大值，φ(-1)=φ(3)=0为最小值，即[0，2]为φ(x)的值域．

本文档预览：3000字符，共9502字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载