考研数学三（微积分）模拟试卷254

考研数学三（微积分）模拟试卷254

选择题

1.设f(x)=e^x在x=0处的2次泰勒多项式为a+bx+cx²，则( )．(B)

A. a=1，b=-1，c=1

B. a=1．b=1，c=1／2

C. a=-1，b=1，c=1

D. a=-1，b=1，c=1／2

解析：e^x=1+x+x²／2+o(x²)=a+bx+cx²+o(x²)，于是a=1，b=1，c=1／2

2.设函数f(x)=ae^x-bx(a＞0)有两个零点，则b／a的取值范围是( )．(D)

A. (0，1／e)

B. (0，e)

C. (1／e，+∞)

D. (e，+∞)

解析：f(x)的定义域为(-∞，+∞)．

显然b＞0，否则f(x)是单调增加函数，与条件矛盾．

f(x)=ae^x-b，令f’(x)=0，得驻点x=lnb／a．

当x∈(-∞，lnb／a)时，f’(x)＜0，则f(x)单调递减．

当x∈(lnb／a，+∞)时，f’(x)＞0，则，(x)单调递增．

当x→-∞时，f(x)→+∞．当x→+∞时，f(x)→+∞．

因此f(lnb／a)是最小值，故当

3.若函数f(x)的二阶导数连续，且满足f’’(x)-f(x)=x，则∫_-π^πf(x)cosdx=( )．(B)

A. f’(π)-f’(-π)

B. 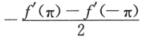C. f(π)-f(-π)

D. 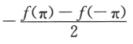解析：∫_-π^πf(x)coscdx=∫_-π^πf(x)d(sinx)=f(x)sinx|_-π^π-∫_-π^πf’(x)sinxdx

=∫_-π^πf’(x)d(cosx)=f’(x)cosx|_-π^π-∫_-π^πf’’(x)cosxdx

=f’(-π)-f’(π)-∫_-π^πf’’(x)cosxdx

=f’(-π)-f’(π)-∫_-π^π[f(x)+x]cosxdx

=f’(-π)-f’(π)-∫_-π^πf(x)cosxdx-∫_-π^πxcosxdx

=f’(-π)-f’(π)-∫_-π^πf(x)cosxdx

移项得∫_-π^πf(x)cosxdx=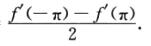

4.设x≥0，y≥0，曲线l₁：x²+y²-xy=1，l₂：x²+y²-xy=2，直线l₃：y=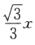，l₄：y=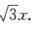区域D₁由l₁，l₂，x=0，y=0围成，D₂由l₁，l₂，l₃，y=0围成，D₃由l₁，l₂，l₄，x=0围成，则对于I_i=(D)

A. I₁＜I₂＜I₃

B. I₃＜I₁＜I₂

C. I₂＜I₃＜I₁

D. I₂＜I₂＜I₃

解析：l₁，l₂，l₃，l₄的图形如图所示．

由于区域D₁关于y=x对称，由轮换对称性得

I₁=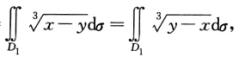

故I₁=0．

由于D₂在y=x的下侧，故y＜x，则本文档预览：3000字符，共11565字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载