考研数学三（微积分）模拟试卷253

考研数学三（微积分）模拟试卷253

选择题

1.已知函数f(x)的一个原函数ln²x，则∫xf′(x)dx=(D)

A. ln²x+C

B. －ln²x+C

C. lnx－ln²x+C

D. 2lnx－ln²x+C

解析：由已知，∫f(x)dx=ln²x+C，f(x)=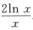

2.已知I=(A)

A. a=5，b=－2．

B. a=－2，b=5．

C. a=2，b=0．

D. a=3，b=－3．

解析：将已知条件改写成

即 I₁=2－a

其中I₁=存在，由此定出参数a与b．

用洛必达法则：

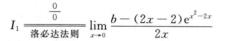
分母极限为0，分子极限为b+2，若b+2≠0，则极限I₁为∞，但极限I₁存在，故必有b+2=0，

即b=－2，于是代入b=－2后该极限为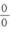型，可用洛必达法则得

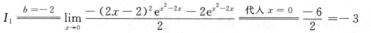
3.设f(x)=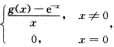(A)

A. f′(0)=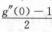B. f′(0)=C. f′(0)=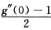D. f′(0)=解析：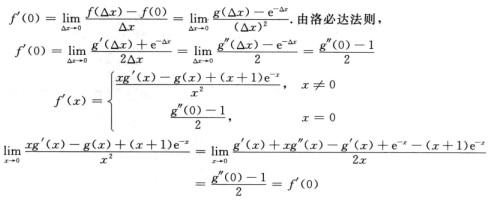

4.设函数f(x)在(－∞，+∞)内有定义，则下述命题中正确的是(D)

A. 若f(x)在(－∞，+∞)内可导且单调增加，则对一切x∈(－∞，+∞)，都有f′(x)＞0

B. 若f(x)在点x₀处取得极值，则f′(x₀)=0

C. 若f″(x₀)=0，则(x₀，f(x₀))是曲线y=f(x)的拐点坐标

D. 若f′(x₀)=0，f″(x₀)=0，f′″(x₀)≠0，则x₀一定不是f(x)的极值点

解析：若在(－∞，+∞)上f′(x)＞0，则一定有f(x)在(－∞，+∞)上单调增加，但可导函数f(x)在(－∞，+∞)单调增加，只能有f′(x))≥0(即可能在某些点上f′(x)=0)，例如f(x)=x³在(－∞，+∞)上单调增加，f′(0)=0．因此不选A．

f(x)若在x₀处取得极值，且f′(x₀)存在，则有f′(x₀)=0，但当f(x)在x₀处取得极值，在x₀处不可导时，就得不到f′(x₀)=0，例如f(x)=｜x｜在x₀=0处取得极小值，它在x₀=0处不可导，因此不选B．

如果f(x)在x₀处二阶导数存在，且(x₀，f(x₀))是曲线的拐点坐标，则f″(x₀)=0，反之不一定，例如f(x)=x⁴在x₀=0处f″(0)=0，但f(x)在(－∞，+∞)没有拐点，因此不选C．由上分析，应选D．

5.设F(x)是f(x)在(a，b)上的一个原函数，则f(x)+F(x)在(a，b)内(C)

A. 可导

B. 连续

C. 存在原函数

D. 是初等函数

解析：因F(x)是f(x)在(a，b)上的一个原函数，所以F′(x)=f(x)，因此F(x)在(a，b)上连续，于是F(x)在(a，b)上存在原函数，从而f(x)+F(x)在(a，b)上存在原函数．因此选C．

6.设n，m为正整数，I_n,m=∫₀¹xⁿln^mxdx是(B)

A. 定积分且值为本文档预览：3000字符，共16459字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载