
考研数学三(概率论与数理统计)模拟试卷89
选择题
1.设随机变量X的概率密度为f(x)= (B)
(B)
A. 1/3
B. 1/2
C. 2
D. 3
解析:由概率密度的性质可知
∫01(c+x)dx=cx+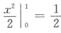
2.设随机变量X~N(1,4),Y~N(0,4),且X,Y相互独立,则D(2X-3Y)=(D)
A. 8
B. 18
C. 24
D. 52
解析:D(X)=4,D(Y)=4,X,Y独立,所以2X与3Y也独立,
D(2X-3Y)=D(2X)+D(3Y)=4D(X)+9D(Y)=4.4+9.4=52.
3.设随机事件A和B满足关系式A∪B=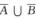 (B)
(B)
A. A-B=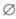 B. AB=
B. AB=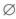 C. AB∪
C. AB∪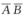 D. A∪
D. A∪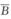 解析:因为A∪B=
解析:因为A∪B= ,所以A∪(A∪B)=A∪
,所以A∪(A∪B)=A∪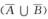
即A∪B=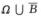 =Ω,因而
=Ω,因而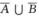 =A∪B=Ω.
=A∪B=Ω.
故 即AB=
即AB=
4.对任意两个互不相容的事件A与B,必有(A)
A. 若P(A)=1,则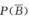 B. 若P(A)=0,则
B. 若P(A)=0,则 C. 若P(A)=1,则
C. 若P(A)=1,则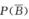 D. 若P(A)=0,则
D. 若P(A)=0,则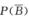 解析:由于AB=
解析:由于AB=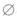 ,就有
,就有 ,也就有P(A)≤
,也就有P(A)≤ .
.
若P(A)=1,则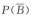 ≥P(A)=1,即
≥P(A)=1,即 =1.答案选A.
=1.答案选A.
若P(A)=0,则只能得到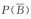
5.设随机变量X在[0,1]上服从均匀分布,记事件A=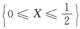 ,B=
,B=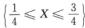 (D)
(D)
A. A与B互斥,但不对立
B. B包含A
C. A与B对立
D. A与B相互独立
解析:
由图形立即得到正确选项为(D),事实上,由题设知
x~f(x)=
