考研数学三（微积分）模拟试卷243

考研数学三（微积分）模拟试卷243

选择题

1.∫₁^eln xdx=(C)

A. e

B. 0

C. 1

D. e+1

解析：∫₁^elnxdx=xlnx｜₁^e－∫₁^e1dx=e－e+1=1．

2.有以下命题：设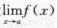=A，不存在，不存在，

①(f(x).g(x))不存在． ②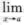(g(x)+h(x))不存在．

③(h(x).g(x))不存在． ④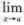(B)

A. 0

B. 1

C. 2

D. 3

解析：举反例说明①②③均错，例如

则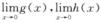均不存在，但

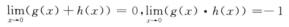
故②③不正确．

若取f(x)=0，则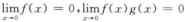，故①也不正确．

按题设，易知不存在．(否则，若存在，

则

3.当x→0时下列无穷小中阶数最高的是

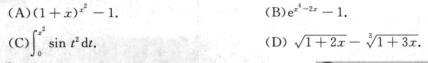(C)

A.

B.

C.

D.

解析：逐一分析它们的阶．

A.(考察等价无穷小)

=x²ln(1+x)～x³(x→0) 是x的三阶无穷小．

B.(考察等价无穷小)

～x⁴－2x～－2x(x→0) 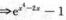是x的一阶无穷小．

C.(待定阶数法)

D.(待定阶数法或泰勒公式法)

或用泰勒公式．已知

(1+t)^α=1+αt+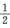α(α－1)t²+o(t²) (t→0)

4.设f(x)=x²e^3x则f⁽ⁿ⁾(0)=(C)

A. 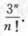B. n²3^n－1

C. 3^n－2n(n－1)

D. 3^n－2(n－1)(n－2)

解析：f(x)=x²e^3x

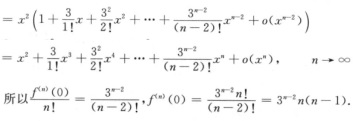
5.设f(x)在[a，b]上连续，在(a，b)内存在二阶导数且f(a)＜0，f(b)＞0，f″(x)＞0．则f(x)在(a，b)内(B)

本文档预览：3000字符，共17349字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载