考研数学三（概率论与数理统计）模拟试卷90

考研数学三（概率论与数理统计）模拟试卷90

选择题

1.设随机变量X服从泊松分布，且E(2－X²)=－4，则P{X＜1}=(B)

A. 0

B. e^－2

C. e^－4

D. e^－1

解析：E(2－X²)=E(2)－E(X²)=2－E(X²)=－4，E(X²)=6．

又因为D(X)=E(X²)－[E(X)]²，设泊松分布的参数为λ，则E(X)=D(X)=λ，故

λ=6－λ²，λ=2，A=－3(舍去)

故X服从泊松分布P(2)．P{X＜1}=P{X=0}=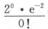

2.设X₁，X₂，X₃，X₄为来自总体N(0，σ²)(σ＞0)的简单随机样本，则统计量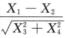(B)

A. N(0，2)

B. t(2)

C. χ²(2)

D. F(2，2)

解析：(1)(X₁－X₂)～N(0，2σ²)，故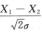～N(0，1)．

(2)均服从N(0，1)，且相互独立，

所以～χ²(2)．

(3)相互独立，故

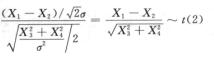
3.设随机事件A与B相互独立，且P(A－B)=0．3，P(B)=0．4，则P(B－A)=(B)

A. 0．1

B. 0．2

C. 0．3

D. 0．4

解析：A，B独立，则A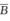，相互独立，，B也相互独立．

0．3=P(A－B)=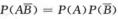=P(A)[1－P(B)]=0．6.P(A)，所以P(A)=0．5．

P(B－A)=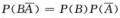

4.设A，B为随机事件，P(B)＞0，则(B)

A. P(A∪B)≥P(A)+P(B)

B. P(A－B)≥P(A)－P(B)

C. P(AB)≥P(A)P(B)

D. P(A｜B)≥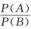解析：这是一道考查概率性质的选择题，应用概率运算性质知，P(A∪B)=P(A)+P(B)－P(AB)≤P(A)+P(B)，选项(A)不成立．P(A－B)=P(A)－P(AB)≥P(A)－P(B)，故正确选项为(B)．而P(A｜B)=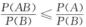，所以(D)不成立．至于选项(C)，它可能成立也可能不成立，例如AB=，P(A)＞0，P(B)＞0，则P(AB)=0＜P(A)P(B)；如果A

5.假设随机变量X的概率密度函数f(x)是偶函数，其分布函数为F(x)，则(C)

A. F(x)是偶函数

B. F(x)是奇函数

C. F(x)+F(－x)=1

D. 2F(x)－F(－x)=1

解析：由于F(x)是单调不减的非负函数，所以(A)(B)不成立．已知f(x)是偶函数，因此有F(－x)=∫_－∞^－xf(t)dt=∫_x^+∞f(t)dt，F(x)+F(－x)=∫_－∞^xf(t)dt+∫_x^+∞f(t)dt=1，选择(C)．而2F(x)－F(－x)=2∫_－∞^xf(t)dt－∫_x^+∞f(t)dt=2－3∫_x^+∞f(t)dt≠1，选项(D)

本文档预览：3000字符，共15700字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载