考研数学三（线性代数）模拟试卷169

考研数学三（线性代数）模拟试卷169

选择题

1.设矩阵A的秩为r，则A中(C)

A. 所有r－1阶子式都不为0

B. 所有r－1阶子式全为0

C. 至少有一个r阶子式不等于0

D. 所有r阶子式都不为0

解析：若矩阵A的秩为r，则A至少有一个r阶子式不等于0，且A的所有r+1阶子式均等于0．故选项(C)正确．

2.已知齐次方程组Ax=0有非零解，且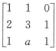A=(A)

A. 2

B. 1

C. 0

D. -1

解析：n个方程n个未知数的齐次方程组Ax=0有非零解 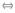｜A｜=0，

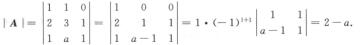
3.多项式f(x)=(B)

A. －1，－1

B. 1，－1

C. －1，1

D. 1，1

解析：行列式是不同行不同列元素乘积的代数和，其一般项是

本题中作为x⁴项，必须每行元素都要有x项出现，因而只能是a₁₄a₂₃a₃₂a₄₁=x⁴，又

ι(4321)=3+2+1=6

于是x⁴的系数为+1．

对于x³项，必须有1行(列)不出现x项，因而只能是

a₁₁a₂₃a₃₂a₄₄=x³

此时ι(1324)=1，从而x³的系数为－1．

或f(x)=

4.设A是n阶可逆矩阵，A^*是A的伴随矩阵，则(A)

A. ｜A^*｜=｜A｜^n－1

B. ｜A^*｜=｜A｜

C. ｜A^*｜=｜A｜ⁿ

D. ｜A^*｜=｜A^－1｜

解析：由AA^*=｜A｜E，有｜AA^*｜=｜A｜E｜，即

｜A｜.｜A^*｜=｜A｜ⁿ｜E｜

A可逆有｜A｜≠0，故｜A^*｜=｜A｜^n－1．

5.设A，B均为n阶可逆矩阵，正确的是(D)

A. (A+B)(A－B)=A²－B²

B. (A+B)^－1=A^－1+B^－1

C. (A+B)²=A²+2AB+B²

D. (AB)^*=B^*A^*

解析：矩阵的乘法没有交换律，A，B可逆不能保证AB=BA，例如

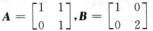
有AB=而BA=，可知(A)(C)均不正确．

A，B可逆时，A+B不一定可逆，即使A+B可逆，其逆一般也不等于A^－1+B^－1．

例如，有(A+B)^－1=

而A^－1+B^－1=

6.已知XA+2E=X+B，其中A=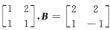，则X=

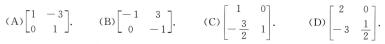(C)

A.

B.

C.

D.

解析：XA+2E=X+B有X(A－E)=B－2E，于是

X=(B－2E)(A－E)^－1

本文档预览：3000字符，共15197字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载