考研数学三（微积分）模拟试卷244
选择题
1.设函数z=
，则dz=
(A)
A.
B.
C.
D.
解析：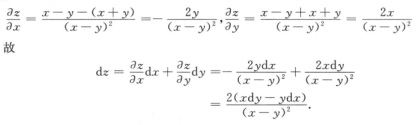
2.设函数f(x)=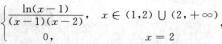
(B)
A. 在(1，2)区间有界．
B. 在(2，+∞)区间有界．
C. 在(1，+∞)区间有界．
D. 在(1，2)和(2，+∞)区间都无界．
解析：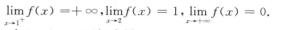
3.设x→a时f(x)与g(x)分别x－a的n阶与m阶无穷小，则下列命题
①f(x)g(x)是x－a的n+m阶无穷小．
②若n＞m，则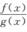
(C)
A. 1
B. 2
C. 3
D. 4
解析：此类问题要逐一分析，按无穷小阶的定义分析：
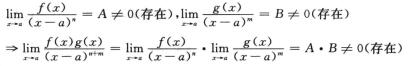
f(x)g(x)是(x－a)的n+m阶无穷小；
又，若n＞m，
是(x－a)的n－m阶无穷小；
因此①②正确．再考察
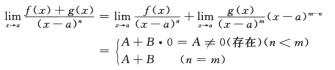
由此得，当n＜m时f(x)+g(x)是x－a的n阶无穷小．
当n=m时f(x)+g(x)是x－a的n阶(A+B≠0)或高于n阶(A+B=0)的无穷小．
例如，x→0时，sinx与－x均是x的一阶无穷小，但
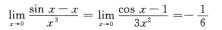
即sinx+(－x)是x的三阶无穷小；因此③不正确．
最后考察
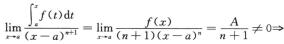
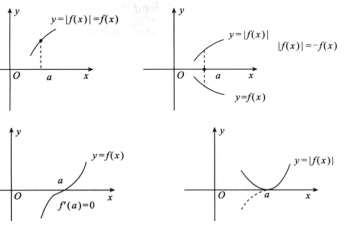
4.设f(x)在点x=a处可导，则函数｜f(x)｜在点x=a处不可导的充分必要条件是(B)
A. f(a)=0，且f′(a)=0．
B. f(a)=0，且f′(a)≠0．
C. f(a)＞0，且f′(a)＞0．
D. f(a)＜0，且f′(a)＜0．
解析：当f(a)≠0时(不论f′(a)是正值还是负值)，由连续性，在x=a附近或｜f(x)｜=f(x)，或｜f(x)｜=－f(x)，于是｜f(x)｜与f(x)在x=a有相同的可导性．由f′(a)存在 
｜f(x)｜′｜x=a存在，(C)(D)被排除．
当f(a)=0，f′(a)=0时曲线y=f(x)在(a，0)点与x轴相切 
y=｜f(x)｜同样在(a，0)点与x轴相切 
｜f(x)｜′｜x=a 存在(且为零值)．(A)被排除．
5.以下四个命题中，正确的是(C)
A. 若f′(x)在(a，b)内连续，则f(x)在(a，b)内有界
B. 若f(x)在(a，b)内连续，则f(x)在(a，b)内有界
C. 若f′(x)在(a，b)内有界，则f(x)在(a，b)内有界
D. 若f(x)在(a，b)内有界，则f′(x)在(a，b)内有界
解析：联系f′(x)与f(x)的是拉格朗日中值定理．取定点x0∈(a，b)，则由拉格朗日中值定理知，
6.下列命题中有一个正确的是
B
解析：(B)正确．
这是线性性质的体现．若f(x)+g(x)在[a，b]上可积，因f(x)在[a，b]上可积，由线性性质知，
g(x)=[f(x)+g(x)]－f(x)
在[a，b]可积，与已知g(x)在[a，b]上不可积矛盾了．因此f(x)+g(x)在[a，b]上不可积．选B．
7.下列叙述错误的是(B)
A. 设f(x)在
本文档预览：3000字符，共16081字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
