考研数学三（概率论与数理统计）模拟试卷91

考研数学三（概率论与数理统计）模拟试卷91

选择题

1.设随机变量X，Y都服从[0，1]上的均匀分布，则E(X+Y)=(A)

A. 1

B. 2

C. 15

D. 0

解析：因为随机变量X，Y都服从[0，1]上的均匀分布，因此有E(X)=E(Y)=．

故E(X+Y)=E(X)+E(Y)=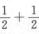

2.一袋中有四只球，编号为1，2，3，4，从袋中一次取出两只球，用X表不取出的两只球的最大号码数，则P{X=4}=(B)

A. 0．4

B. 0．5

C. 0．6

D. 0．7

解析：这是一个古典型概率P{X=4}=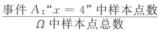

取球有先后次序，取了两个总共有可能n=4.3．

x=4，取一个为4号，另一个为1，2，3中一个，共有可能1.3，再考虑先后，应有总的可能n_A=2.1.3，

故P{X=4}=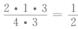

3.将一枚硬币独立投掷两次，记事件A=“第一次掷出正面”，B=“第二次掷出反面”，C=“正面最多掷出一次”，则事件(B)

A. A，B，C两两独立

B. A与BC独立

C. B与AC独立

D. C与AB独立

解析：由题设知，试验的基本事件共有4个：ω₁=“正，正”，ω₂=“正，反”，ω₃=“反，正”，ω₄=“反，反”，所以A=“ω₁，ω₂”，B=“ω₂，ω₄”，C=“ω₂，ω₃，ω₄”，P(A)=P(B)=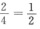，P(C)=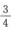，显然A与B独立，，故B，C不独立，选项(A)不成立．

又BC=B，ABC=AB，P(ABC)==P(AB)=P(A)P(B)=P(A)P(BC)，即A与BC独立，选项(B)正确．

而P(ABC)=P(A)P(B)=≠P(B)P(AC)=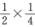，P(ABC)=≠P(C)P(AB)=

4.设随机事件A，B，满足P(A)＞0，P(B｜A)=1，则(C)

A. B=Ω

B. A－B=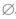C. P(A－B)=0

D. P(B－A)=0

解析：P(B｜A)=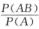

5.假设随机变量X的分布函数为F(x)，概率密度函数f(x)=af₁(x)+bf₂(x)，其中f₁(x)是正态分布N(0，σ²)的概率密度函数，f₂(x)是参数为λ的指数分布的概率密度函数，已知F(0)=1／8，则(D)

A. a=1，b=0

B. a=3／4，b=1／4

C. a=1／2，b=1／2

D. a=1／4，b=3／4

解析：由∫_－∞^+∞f(x)dx=a∫_－∞^+∞f₁(x)dx+b∫_－∞^+∞f₂(x)dx=a+b=1，知四个选项均符合这个要求，因此只好通过F(0)=确定正确选项．

由于F(0)=∫_－∞⁰f(x)dx=a∫_－∞⁰f₁(x)dx+b∫_－∞⁰f₂(x)dx=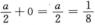

所以a=

6.设随机变量X的分布函数和概率密度函数分别为F(x)和f(x)，则随机变量－X的分布函数和概率密度函数分别为(C)

A. F(－x)和f(－x)

B. F(－x)

本文档预览：3000字符，共14774字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载