考研数学三（微积分）模拟试卷251

考研数学三（微积分）模拟试卷251

选择题

1.设函数f(x)可导且f′(1)=0．5，则y=f(x²)在x=－1处的微分dy｜_x=－1=(A)

A. －dx

B. 0

C. dx

D. 2dx

解析：记u=x²4，则x=－1时u=1，

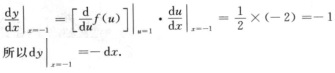
2.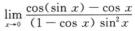(C)

A. 1

B. 1／2

C. 1／3

D. 0

解析：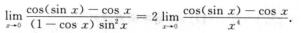

由三角函数公式可知，cos(sinx)－cosx=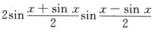，所以当x→0时，

cos(sinx)－cosx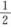～(x+sinx)(x－sinx)

3.设f(x)=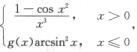(C)

A. 极限不存在

B. 极限存在，但不连续

C. 连续，但不可导

D. 可导

解析：先分别考察左、右可导性．

显然，f(0)=0．

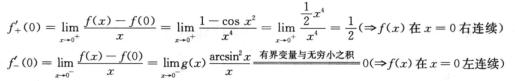
4.设f(x)具有二阶连续导数，且f′(1)=0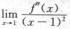，(B)

A. f(1)是f(x)的极大值

B. f(1)是f(x)的极小值

C. (1，f(1))是曲线f(x)的拐点坐标

D. f(1)不是f(x)的极值，(1，f(1))也不是曲线f(x)的拐点坐标

解析：因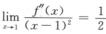＞0，由极限的保号性质，存在δ＞0，当0＜｜x－1｜＜δ时

5.曲线y=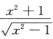(D)

A. 既有铅直又有水平与斜渐近线

B. 仅有铅直渐近线

C. 只有铅直与水平渐近线

D. 只有铅直与斜渐近线

解析：只有间断点x=±1

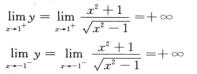
x=1与x=－1为铅直渐近线．

6.I=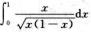(B)

A. π

B. π／2

C. π／4

D. π／8

解析：分母先配方后再作平移变换

7.下列反常积分发散的是

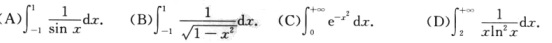(A)

A.

B.

C.

D.

解析：方法1：x=0是(A)的瑕点．

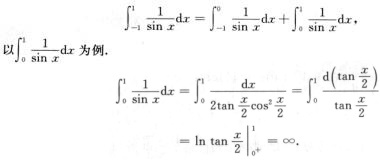
所以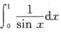发散，从而知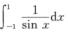发散．选A．

方法2：用比较判别法，

因x→0时sinx～x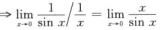，=1．

又本文档预览：3000字符，共18347字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载