考研数学三（微积分）模拟试卷246

考研数学三（微积分）模拟试卷246

选择题

1.当n→∞时，数列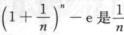(D)

A. 高阶无穷小

B. 低阶无穷小

C. 等价无穷小

D. 同阶但非等价无穷小

解析：该题就是要计算极限

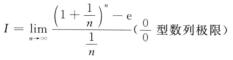
直接转化为求型函数极限，然后用洛必达法则．

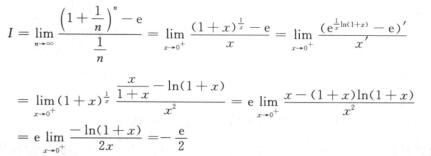
2.以下函数f(g(x))以x=0为第二类间断点的是

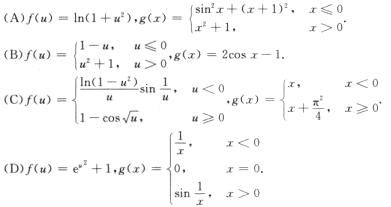(D)

A.

B.

C.

D.

解析：易知(A)，(B)中，f(u)在(－∞，+∞)内连续，g(x)在(－∞，+∞)内连续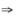复合函数f(g(x))在(－∞，+∞)内连续．因此只须在(C)，(D)中选择．

考察(C)

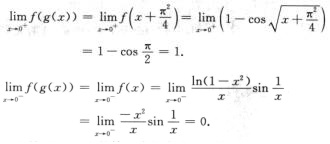
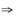
3.设f(x)为连续函数，g(x)=∫_－x⁰tf(x+t)dt，则g′(x)=(A)

A. －∫₀^xf(u)du．

B. ∫₀^xf(u)du．

C. －∫₀^－xf(u)du．

D. ∫₀^－xf(u)du．

解析：作变量代换u=x+t，则

g(x)=∫_－x⁰tf(x+t)dt=∫₀^x(u－x)f(u)du=∫₀^xuf(u)du－x∫₀^xf(u)du

g′(x)=xf(x)－∫₀^xf(u)du－xf(x)=－∫₀^xf(u)du．

4.函数y=f(x)在(－∞，+∞)内连续，其二阶导函数的图形如图所示，则y=f(x)的拐点的个数是

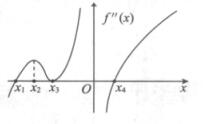(C)

A. 1

B. 2

C. 3

D. 4

解析：只须考察f″(x)=0的点与f″(x)不存在的点．

f″(x₁)=f″(x₄)=0，在x=x₁，x₄两侧f″(x)变号，故凹凸性相反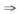

5.下述结论不正确的是

(C)

A.

B.

C.

D.

解析：下面来证明(C)不正确．

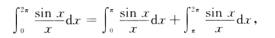
对于第2个积分，作变量变换，令x=π+t，当x=π时t=0；x=2π时t=π，于是

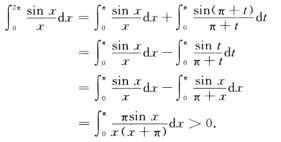
6.函数F(x)=∫_x^x+πln(1+cos²t)cos2tdt(A)

A. 为正数

B. 为负数

C. 恒为零

D. 不是常数

解析：因被积函数是以π为周期的函数，它在每个周期上的积分值相等，因此，

F(x)=F(0)=∫₀^πln(1+cos²t)cos2tdt=∫₀^πln(1+cos²t)dsin2t

7.已知y₁(x)和y₂(x)是方程y′+p(x)y=0的两个不同的特解，则该方程的通解为(D)

A. y=Cy₁(x)

B. y=

本文档预览：3000字符，共16767字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载